Abgebrochene Glasplatte - Optimierungsaufgabe

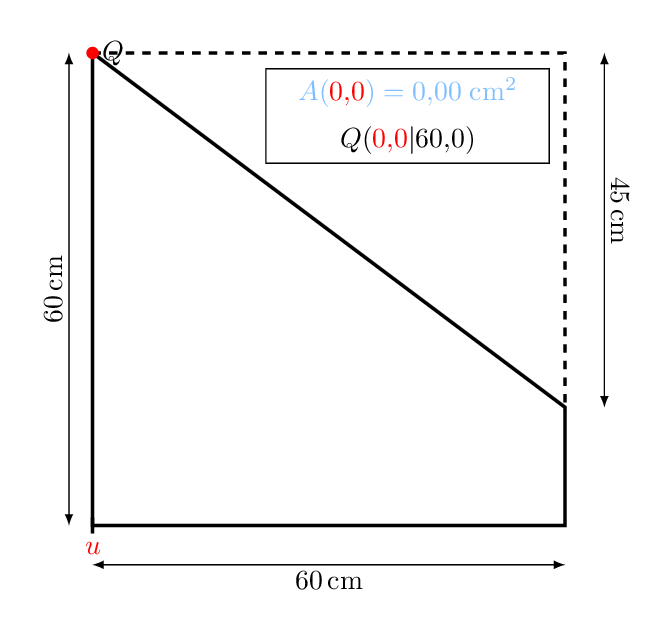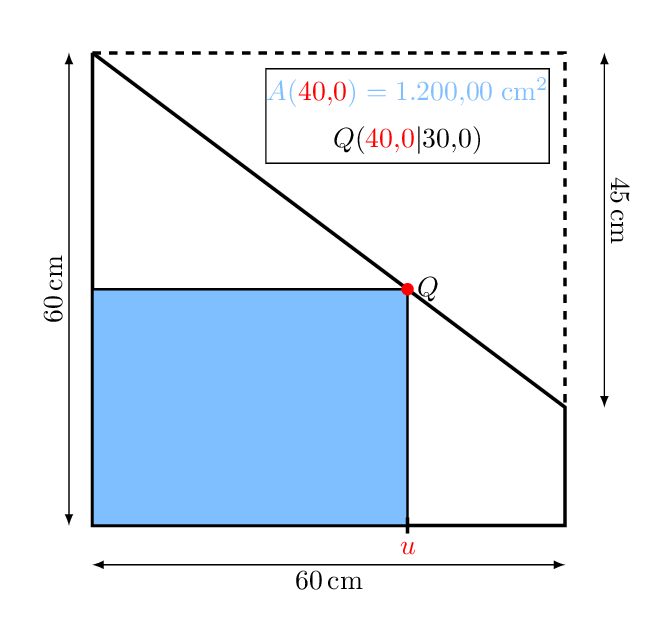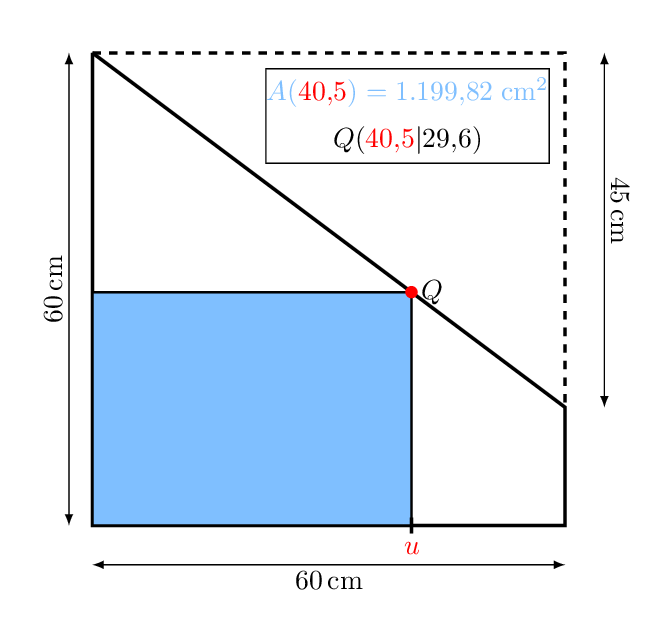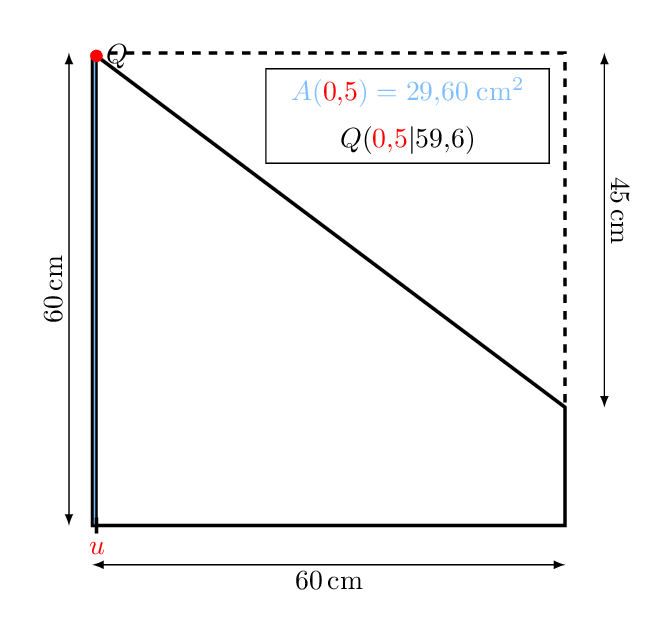
Erster Schritt: Variablen festlegen:

Länge der Grundseite $u$ in $cm$ mit $0 \le x \le 60$.

Zweiter Schritt: Nebenbedingungen formulieren:

Der rechte obere Eckpunkt des Rechtecks liegt auf der Geraden, die die Bruchkante beschreibt: $h = \frac{-45}{60} \cdot u + 60 = -\frac{3}{4}\cdot u + 60$

Dritter Schritt: Zielfunktion aufstellen:

Der Flächeninhalt $A=g \cdot h$ soll maximal werden:
$A(u) = u \cdot (-\frac{3}{4} u + 60) = -\frac{3}{4}u^2+60u$

Vierter Schritt: Optimierung der Zielfunktion:

Das Schaubild von $A(u)$ zeigt eine nach unten geöffnete Parabel zweiter Ordnung, ihr Maximum findet sich also im Scheitelpunkt. Dieser kann z.B. mit der Formel gefunden werden:
$u_{max} = -\frac{b}{2\cdot a}=-\frac{60}{2\cdot (-\frac{3}{4})}=40$
Natürlich können die Koordinaten des Scheitelpunkts auch mit anderen Methoden berechnet werden, etwa durch quadratische Ergänzung, als Mittelwert der beiden Nullstellen oder mit Hilfe der Differentialrechnung.
Die Höhe der flächeinhaltsgrößten Glasplatte bekommt man am einfachsten mit der Nebenbedingung:
$h_{max} = -\frac{3}{4}\cdot 40 + 60 = 30$
Und den dazugehörigen Flächeninhalt über $A(u)$:
$A_{max}=A(40)=-\frac{3}{4}40^2+60\cdot 40=1200$

Fünfter Schritt: Randwertbetrachtung:

Da es sich beim Schaubild von $A(u)$ um eine nach unten geöffnete Parabel zweiter Ordnung handelt hat dieses in jedem Fall ein absolutes Maximum im Scheitelpunkt.
Alternativ:
$A(0) = 0$ und
$A(60) = -\frac{3}{4}60^2+60\cdot 60 = 900 < A(40)$

Sechster Schritt: Interpretation im Sachzusammenhang:

Die größtmögliche rechteckige Glasscheibe ist $40\; cm$ breit, $30\; cm$ hoch und hat eine Fläche von $1200\; cm^2$