03.11.2022
Chain of Cubes
23 cubes have been fitted together exactly face to face, to nearly make one complete loop.
What is the smallest number of extra cubes needed to complete it?


Lösung
Meine Lösung lautet 5.
 Es gibt natürlich noch mehr Lösungsmöglichkeiten. Aber eine mit weniger als 5 zusätzlichen Würfeln habe ich nicht gefunden.
Es gibt natürlich noch mehr Lösungsmöglichkeiten. Aber eine mit weniger als 5 zusätzlichen Würfeln habe ich nicht gefunden.
16.10.2022
Einstiegsbeispiel: Wahlergebnis
Für die Kommunalwahl am kommenden Sonntag hat eine kandidierende Partei eine Umfrage durchgeführt. Dabei wurden 1000 Personen befragt und 373 gaben an, diese Partei zu wählen.
Die Frage ist, mit wie viel Prozent der Stimmen die Partei bei der Wahl rechnen kann.
Als wahrscheinlichsten Wert würde man 37,3% annehmen, da dies genau der relativen Häufigkeit h aus der Umfrage entspricht. (Dies nennt man eine Punktschätzung )
Genauer betrachtet sucht man eine unbekannte Wahrscheinlichkeit p, hier das Wahlergebnis am Sonntag. In der Praxis gibt man gerne ein Intervall an, in dem der Schätzwert (hier das Umfrageergebnis) mit hoher Wahrscheinlichkeit liegt, ein sogenanntes
Vertrauensintervall oder auch Konfidenzintervall genannt. Ein gängiger Wert ist das 95%-Vertrauensintervall , das Intervall für p, in dem der Schätzwert mit 95%-iger Wahrscheinlichkeit liegt.
Die Sigma-Regel sagt uns, dass die beobachtete Trefferzahl (hier 373) mit 95%-iger Wahrscheinlichkeit im Intervall
\[ [ \mu - 1{,}96 \cdot\sigma \quad; \quad\mu + 1{,}96 \cdot\sigma ] \]
liegt. Durch einige Umformungen und Näherungen, die ich später einfügen werde, erhält man als Näherungswert für das Vertrauensintervall:
\[ \tiny h - 1{,}96\cdot\sqrt{\frac{h\cdot(1-h)}{n}} \quad \le \quad p \quad \le \quad h + 1{,}96\cdot\sqrt{\frac{h\cdot(1-h)}{n}} \]
Für das Beispiel ergibt sich somit, dass die Partei bei der Wahl am Sonntag mit einer Wahrscheinlichkeit von 95% zwischen 34,3% und 40,3% erhält.
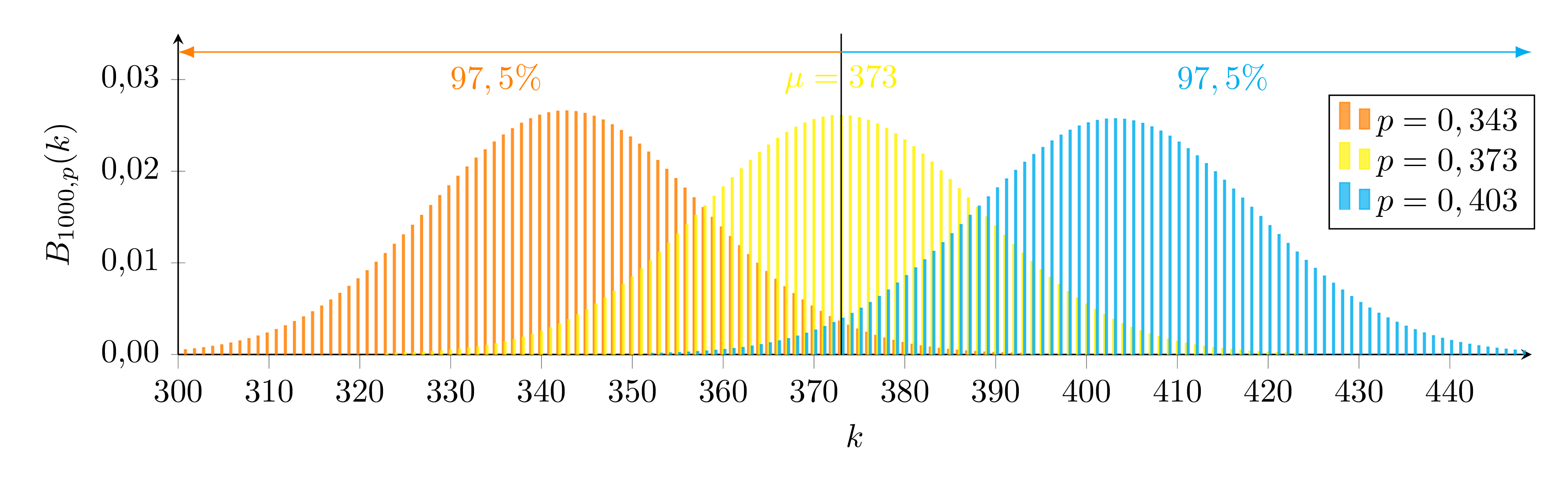 Grafisch bedeutet dies, dass der Schätzwert 373 gerade außerhalb des 97,5%-Bereichs der orangenen Verteilung und gerade unterhalb des 2,5%-Bereichs der blauen Verteilung liegt.
Grafisch bedeutet dies, dass der Schätzwert 373 gerade außerhalb des 97,5%-Bereichs der orangenen Verteilung und gerade unterhalb des 2,5%-Bereichs der blauen Verteilung liegt.
Exakt bestimmen kann man dieses Intervall so:
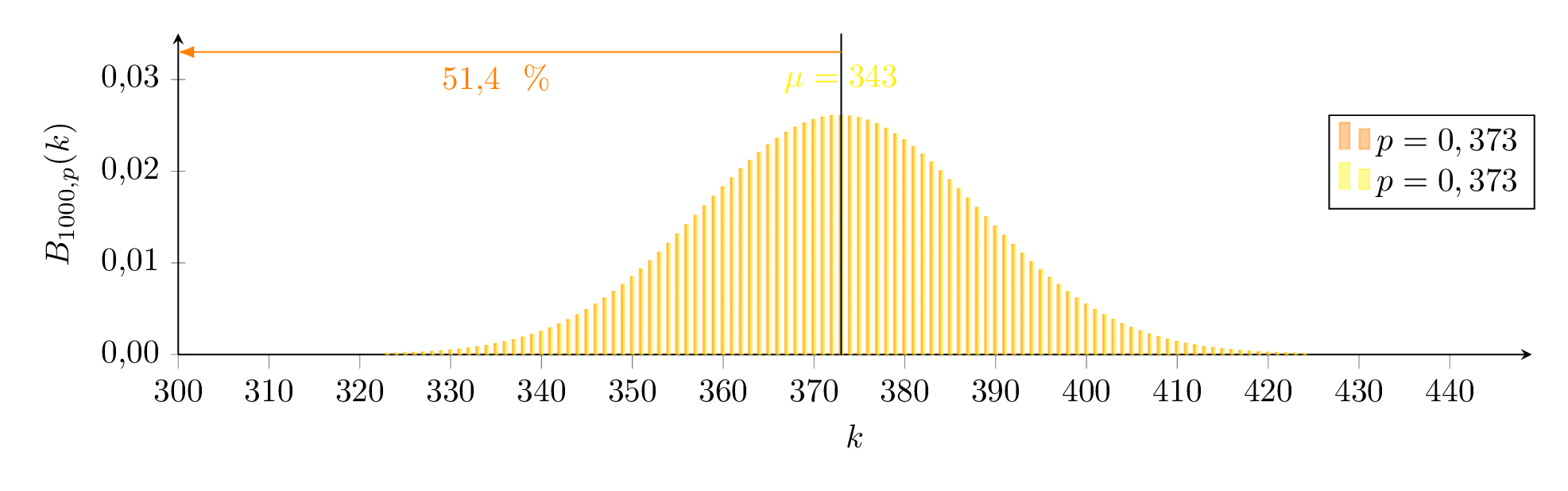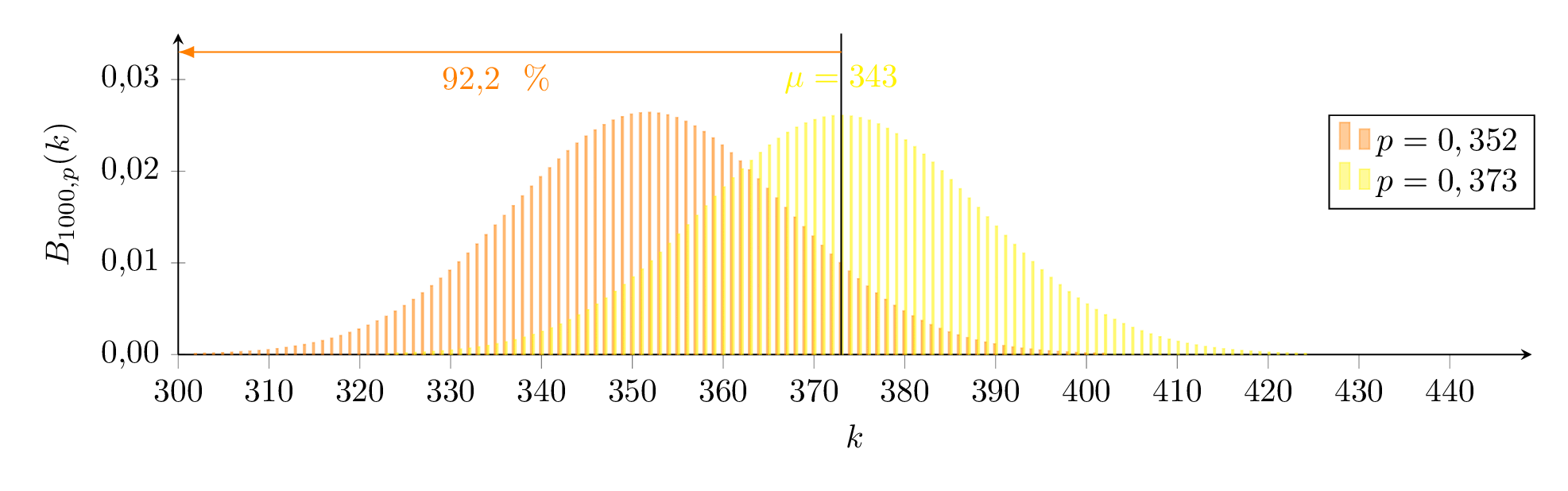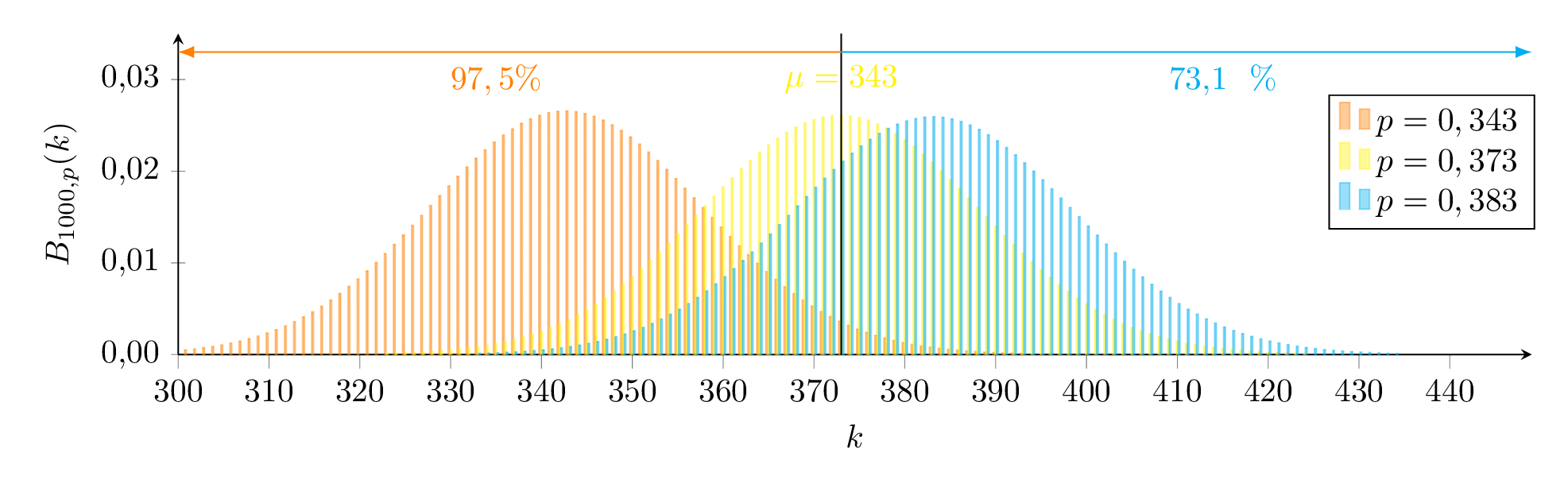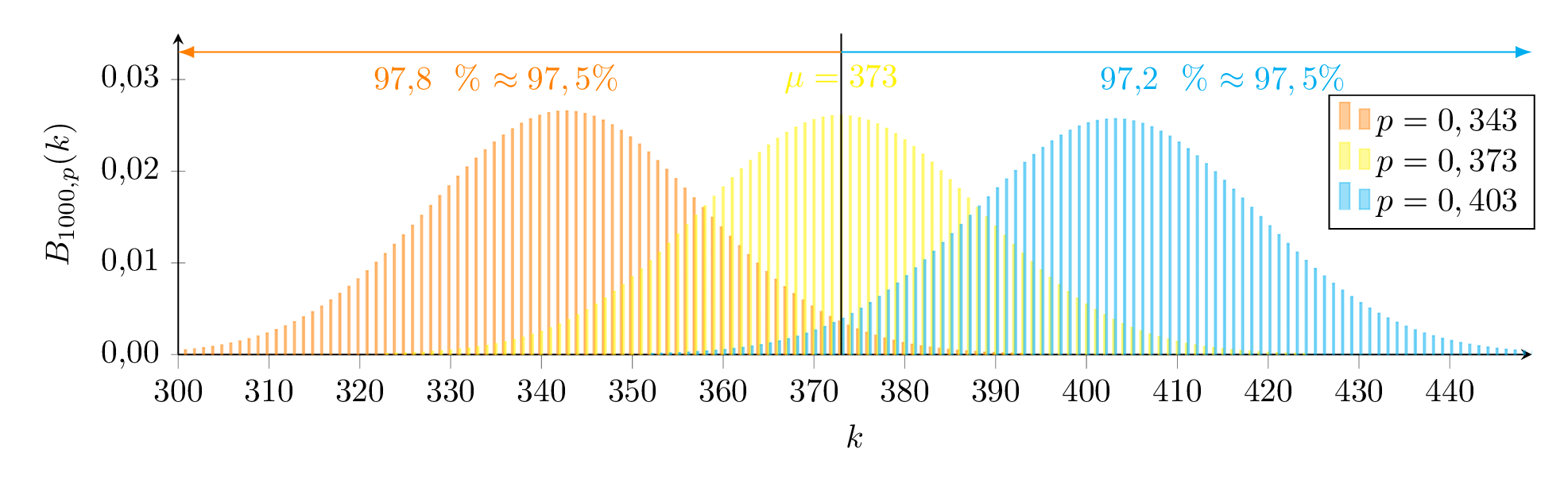 Wir suchen also eine Binomialverteilung für die Untergrenze p1 (orange) so, dass B1000;p1(X≤373)≥97,5 gilt und eine für die Obergrenze p2 (blau) so, dass B1000;p2(X≥373)≥97,5 gilt.
Da man die Formel für die kummulierte Wahrscheinlichkeit bei der Binomialverteilung nicht nach p auflösen kann, muss man sich mit dem Taschenrechner (oder dem Computer) durch gezieltes Ausprobieren diesen Werten nähern.
Wir suchen also eine Binomialverteilung für die Untergrenze p1 (orange) so, dass B1000;p1(X≤373)≥97,5 gilt und eine für die Obergrenze p2 (blau) so, dass B1000;p2(X≥373)≥97,5 gilt.
Da man die Formel für die kummulierte Wahrscheinlichkeit bei der Binomialverteilung nicht nach p auflösen kann, muss man sich mit dem Taschenrechner (oder dem Computer) durch gezieltes Ausprobieren diesen Werten nähern.
Wir sind mit unserem Forschungsschiff auf einer abgelegenen Südseeinsel gelandet, die von einer eingeführten Kaninchenpopulation beherrscht wird. Wir wollen abschätzen, wie viele der Tiere die Insel bevölkern. Dazu fangen wir 50 Kaninchen, markieren sie und lassen sie wieder laufen, in der Hoffnung, dass diese sich gleichmäßig über der Insel verteilen. Einige Tage später fangen wir erneut 50 Kaninchen und zählen darunter 18 markierte Individuen.
Nun wollen wir mit Hilfe des 95%-Konfidenzintervalls für die beobachtete relative Häufigkeit der markierten Kaninchen abschätzen, wie groß die Kaninchenpopulation ist.
Lösung:
Als erste Schätzung gehen wir davon aus, dass unsere beobachtete relative Häufigkeit h=5018=0,36=36% der Wahrscheinlichkeit p entspricht. Dies würde zu N0=0,3650≈139 Kaninchen führen.
Die beobachtete relative Häufigkeit ist aber nur ein Punktschätzung für den wahren Anteil p unter den Kaninchen auf der Insel. Wir suchen ein Untergrenze p1 udn eine Obergrenze p2 zwischen denen die beobachtete relative Häufigkeit h mit 95%-iger Wahrscheinlichkeit liegt, also zwei Binomialverteilungen an deren oberer 97,5% - Grenze bzw. an deren unterer 2,5% - Grenze h liegt. (2,5% bzw. 97,5% deshalb, weil von den restlichen 5% des 95%-Intervalls die Hälfte ober- und die andere Hälfte unterhalb des Vertrauensbereichs vermutet wird).
Da die Zahlen eher gering sind, nutzen wir nicht die Näherung sondern tasten uns exakt an die Grenzen heran:
Für die Untergrenze (für p) muss gelten, dass 97,5% der Ergebnisse unterhalb von 18 Kaninchen liegen, also
\[ B_{50,p_1}(X<18) \ge 97{,}5 \%
\]
ist. Lässt man sich jetzt für verschiedene Werte von p kumulierte Binomialverteilungen berechnen erhält man:
| $$p_1$$ |
$$F_{50, p_1}(17)$$ |
| 0,229 |
0,97516 |
| 0,230 |
0,97411 |
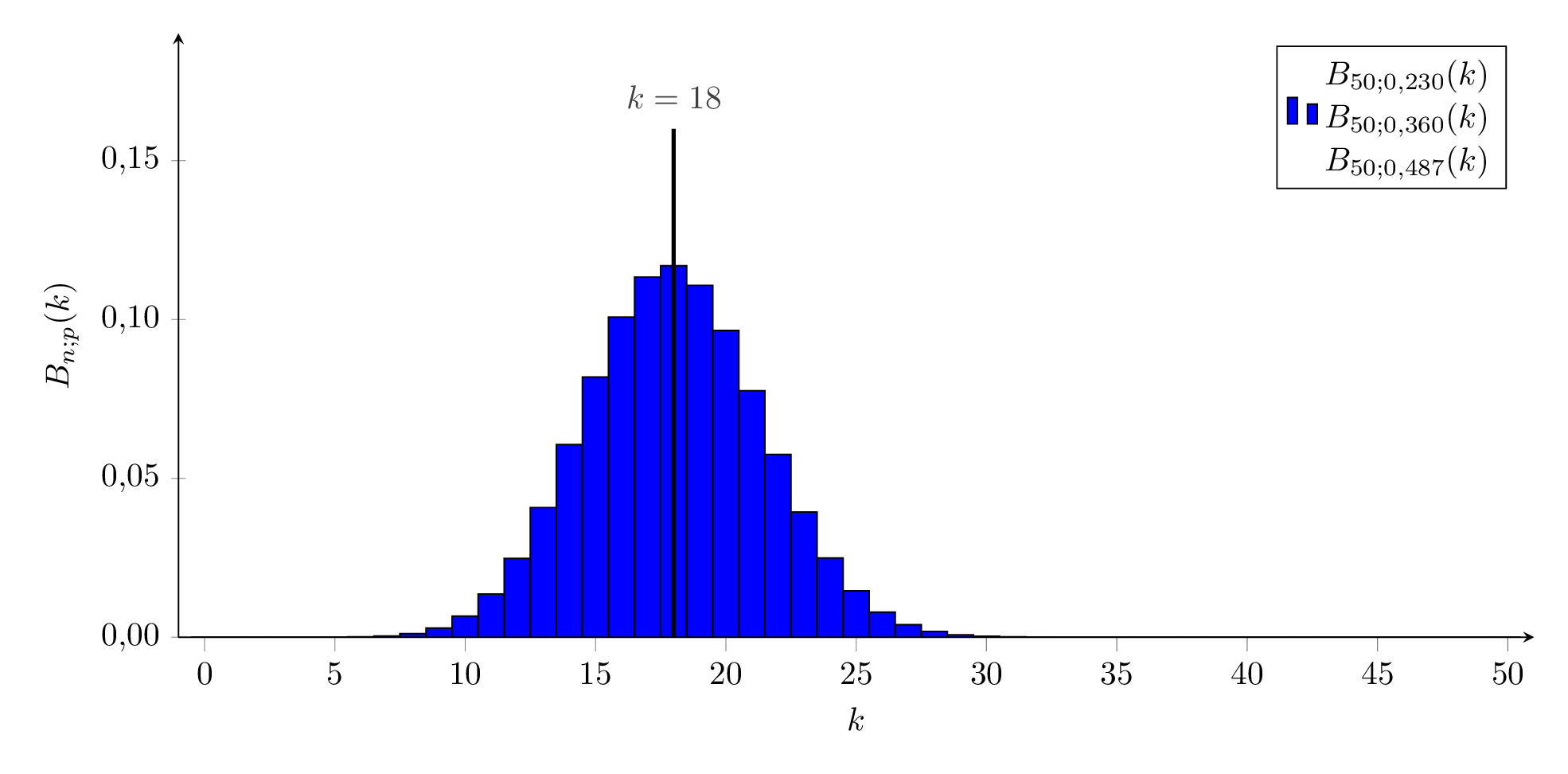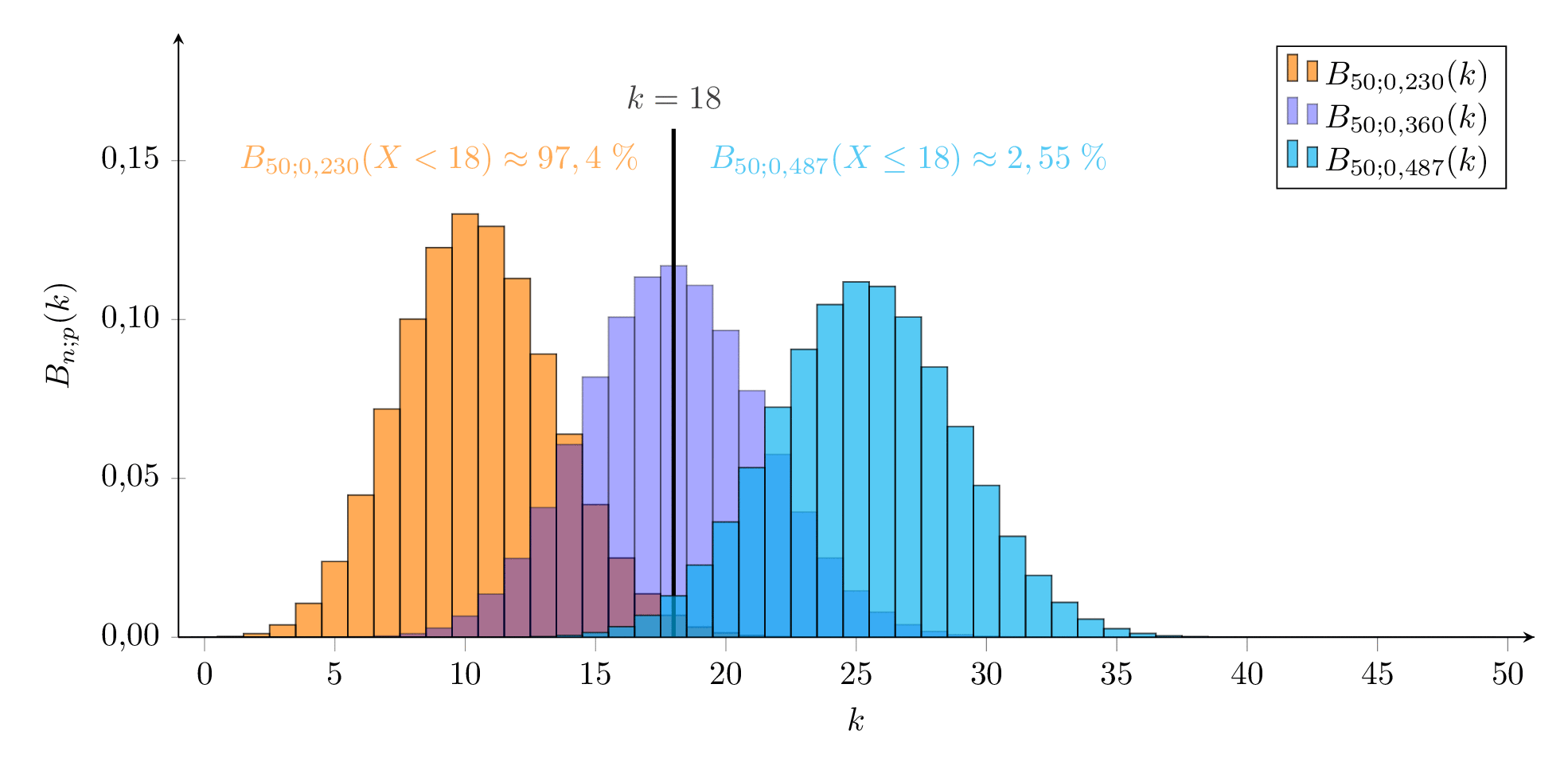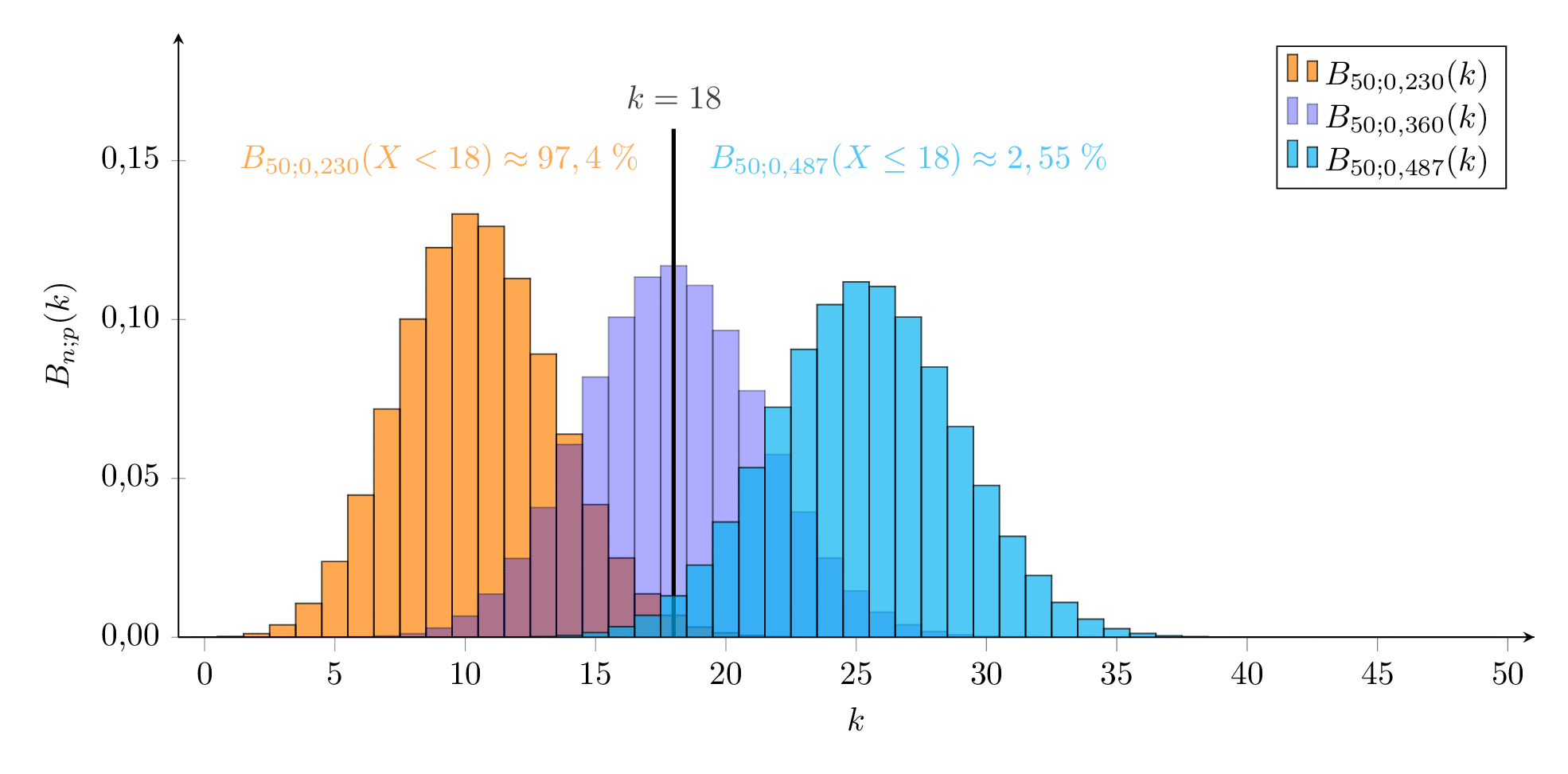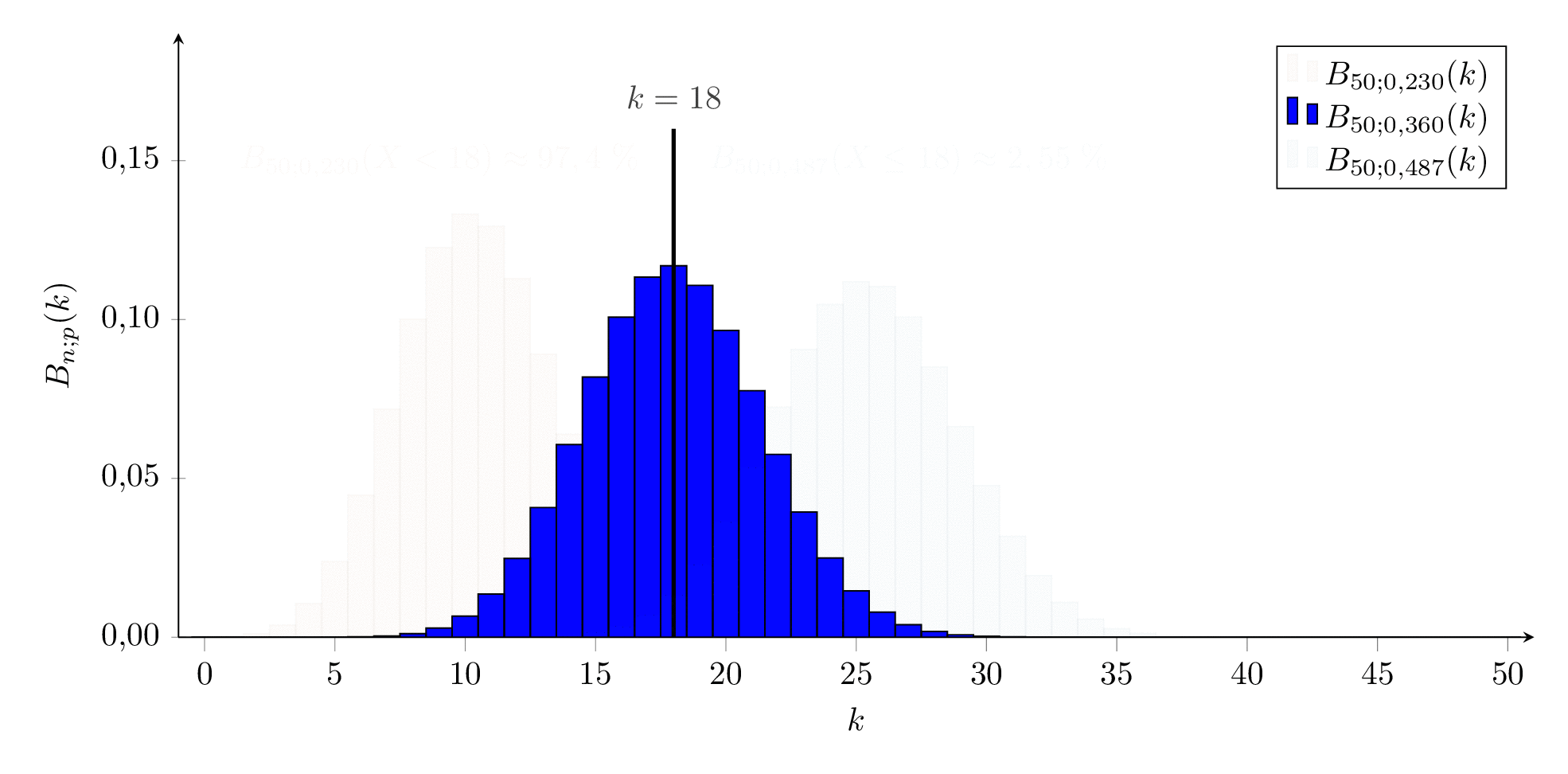
p1≈0,230 ist also die kleinste Wahrscheinlichkeit, bei der unsere beobachtete Anzahl an markierten Kaninchen noch im 95% - Vertrauensintervall liegt. Dies ergibt eine Obergrenze für die Anzahl an Individuen von N1=0,23050≈217.
Analog suchen wir für die Obergrenze der Wahrscheinlichkeit einen Wert für p2 so, dass die beobachtete Anzahl noch gerade im 95% - Vertrauensintervall liegt, also
\[ B_{50,p_2}(X \le 18) \ge 2{,}5 \%
\]
Hier erhält man
| $$p_2$$ |
$$F_{50, p_1}(18)$$ |
| 0,487 |
0,02554 |
| 0,488 |
0,02472 |
0,487 bzw. 48,7% ist also der größte Wert für die Wahrscheinlichkeit, mit der unsere beobachtete Häufigkeit noch zu 95% verträglich ist. Dies ergibt eine Untergrenze für die Population von N2=0,48750≈103.
Wir können also mit einer Wahrscheinlichkeit von 95% davon ausgehen, dass zwischen 103 und 217 Kaninchen auf der Insel leben. Das Ergebnis scheint sehr ungenau zu sein, lässt aber immerhin eine solide Abgrenzung der Größenordnung (‘wenige Hundert’) zu.
Die beiden ‘Grenzverteilungen’ sind in der folgenden Animation orange bzw. cyan dargestellt, die mit p=h=0,360 in blau.
 Mit der Näherungsformel (deren Einsatz hier wegen der kleinen Zahl fragwürdig ist) ergibt sich für die Grenzen der Wahrscheinlichkeit
\[ \begin{align*} p_{o/u} &= h \pm c\cdot\sqrt{\frac{h(1-h)}{n}}\\[5pt]
p_{o/u} &= 0{,}360 \pm 1{,}96\cdot\sqrt{\frac{0{,}36(1-0{,}36)}{50}}\\[5pt]
p_{o/u} &\approx 0{,}360 \pm 0{,}133
\end{align*}\]
also pu=0,227 und po=0,493. In Populationszahlen bedeutet dies:
Mit der Näherungsformel (deren Einsatz hier wegen der kleinen Zahl fragwürdig ist) ergibt sich für die Grenzen der Wahrscheinlichkeit
\[ \begin{align*} p_{o/u} &= h \pm c\cdot\sqrt{\frac{h(1-h)}{n}}\\[5pt]
p_{o/u} &= 0{,}360 \pm 1{,}96\cdot\sqrt{\frac{0{,}36(1-0{,}36)}{50}}\\[5pt]
p_{o/u} &\approx 0{,}360 \pm 0{,}133
\end{align*}\]
also pu=0,227 und po=0,493. In Populationszahlen bedeutet dies:
Als Untergrenze 0,49350≈101 und als Obergrenze 0,22750≈220.
Wie groß sollte die Stichprobe sein?
Wir wollen auf fünf Prozentpunkte genau ermitteln, mit welchem Ergebnis wir bei der Wahl am kommenden Sonntag (mit einer Wahrscheinlichkeit von 95 %) rechnen können. Dazu wollen wir in der Fußgängerzone eine Umfrage durchführen. Zur Planung wäre es hilfreich zu wissen, wie viele Passanten wir befragen müssen.
Nun, das 95 % -Vertrauensintervall hat eine Breite/Länge von
\[ l = 2\cdot c \cdot \sqrt{\frac{h\cdot(1-h)}{n}}
\]
also den doppelten Abstand vom Mittelwert zur 95 % - Grenze. Wir wollen das Ergebnis auf ±5% genau wissen, das Vertrauensintervall soll also höchstens l=10%=0,1 breit sein.
Die obige Gleichung können wir nach dem Stichprobenumfang n auflösen:
\[ n = \frac{4\cdot c^2}{l^2}\cdot h\cdot(1-h)
\]
Dies ist die Mindestanzahl an Personen, die wir fragen müssen um mit 95 %-iger Sicherheit ein Ergebnis mit einer maximalen Ungenauigkeit von ±5% zu erhalten:
\[ n \ge \frac{4\cdot c^2}{l^2}\cdot h\cdot(1-h) \quad\quad (\ast)
\]
Dummerweise haben wir noch keine Idee, wie groß unser Schätzwert (unsere Punktschätzung) h ist.
Gehen wir einfach mal vom ungünstigsten Fall aus. Der Term h⋅(1−h) hat ein absolutes Maximum von 0,25 bei h=0,5 (siehe Abbildung).
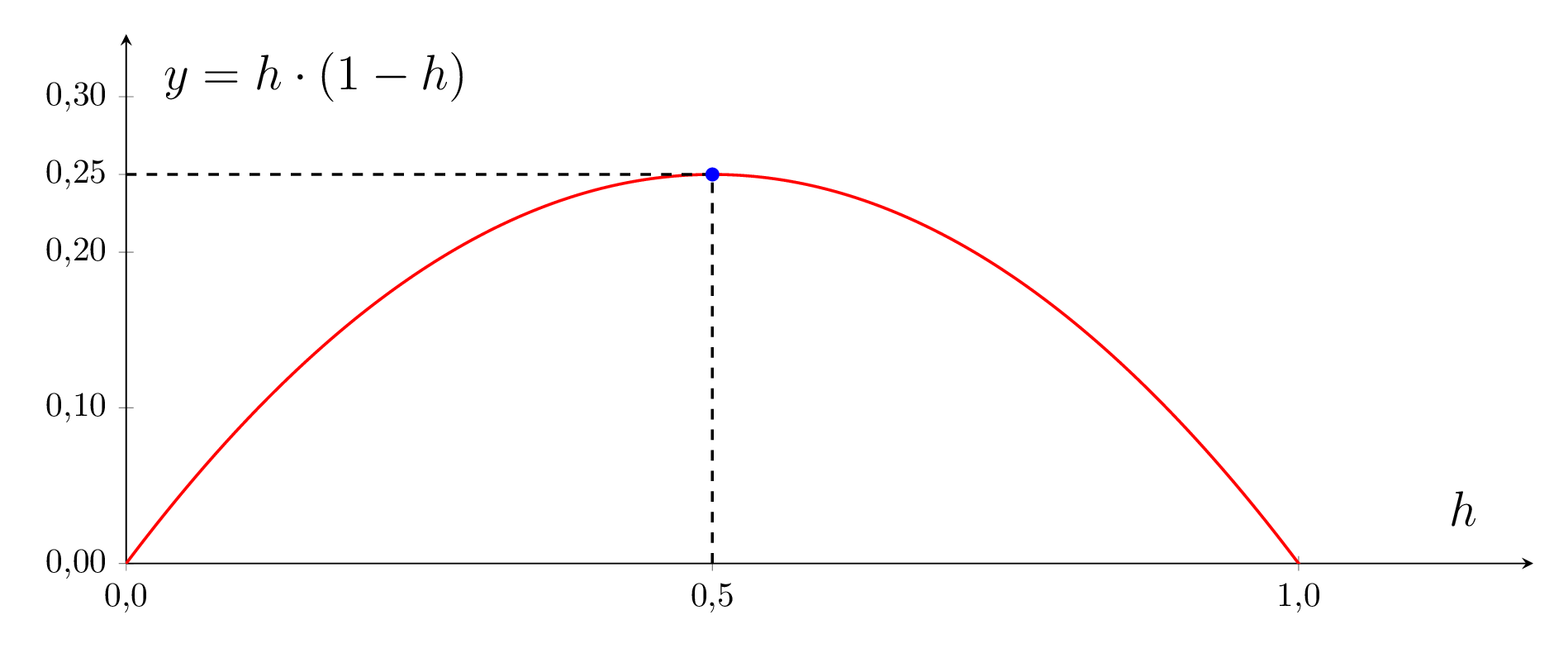 Im schlimmsten Fall müssen wir also
\[ n \ge \frac{4\cdot c^2}{l^2}\cdot 0{,}25=\frac{c^2}{l^2}
\]
Personen fragen. Da wir eine 95 %-ige Sicherheit haben wollen ist c=1,96 und wir wollen es auf 5 % genau haben, also l=0,1 und somit müssen wir
\[ n \ge \frac{1{,}96^2}{0{,}1^2} = 384{,}16
\]
also mindestens 385 Passanten befragen um mit mehr als 95 %-iger Wahrscheinlichkeit ein auf ±5% genaues Ergebnis zu erhalten.
Im schlimmsten Fall müssen wir also
\[ n \ge \frac{4\cdot c^2}{l^2}\cdot 0{,}25=\frac{c^2}{l^2}
\]
Personen fragen. Da wir eine 95 %-ige Sicherheit haben wollen ist c=1,96 und wir wollen es auf 5 % genau haben, also l=0,1 und somit müssen wir
\[ n \ge \frac{1{,}96^2}{0{,}1^2} = 384{,}16
\]
also mindestens 385 Passanten befragen um mit mehr als 95 %-iger Wahrscheinlichkeit ein auf ±5% genaues Ergebnis zu erhalten.
Wenn wir davon ausgehen können, dass wir ca. 20 % der Stimmen bekommen, unsere Punktschätzung also 0,2 ist, dann können wir direkt die obige Formel (∗) nutzen
\[ \begin{align*} n & \ge \frac{4\cdot c^2}{l^2}\cdot h \cdot(1-h) \\[5pt]
n & \ge \frac{4\cdot 1{,}96^2}{0{,}1^2}\cdot 0{,}2\cdot(1-0{,}2) \approx 245{,}9
\end{align*}
\]
und müssen “nur” 246 Passanten befragen, um die gleiche Genauigkeit zu erhalten.
08.10.2022
Aussehen der Binomialverteilung:
Die Binomialverteilung hängt von den Parametern n und p ab.
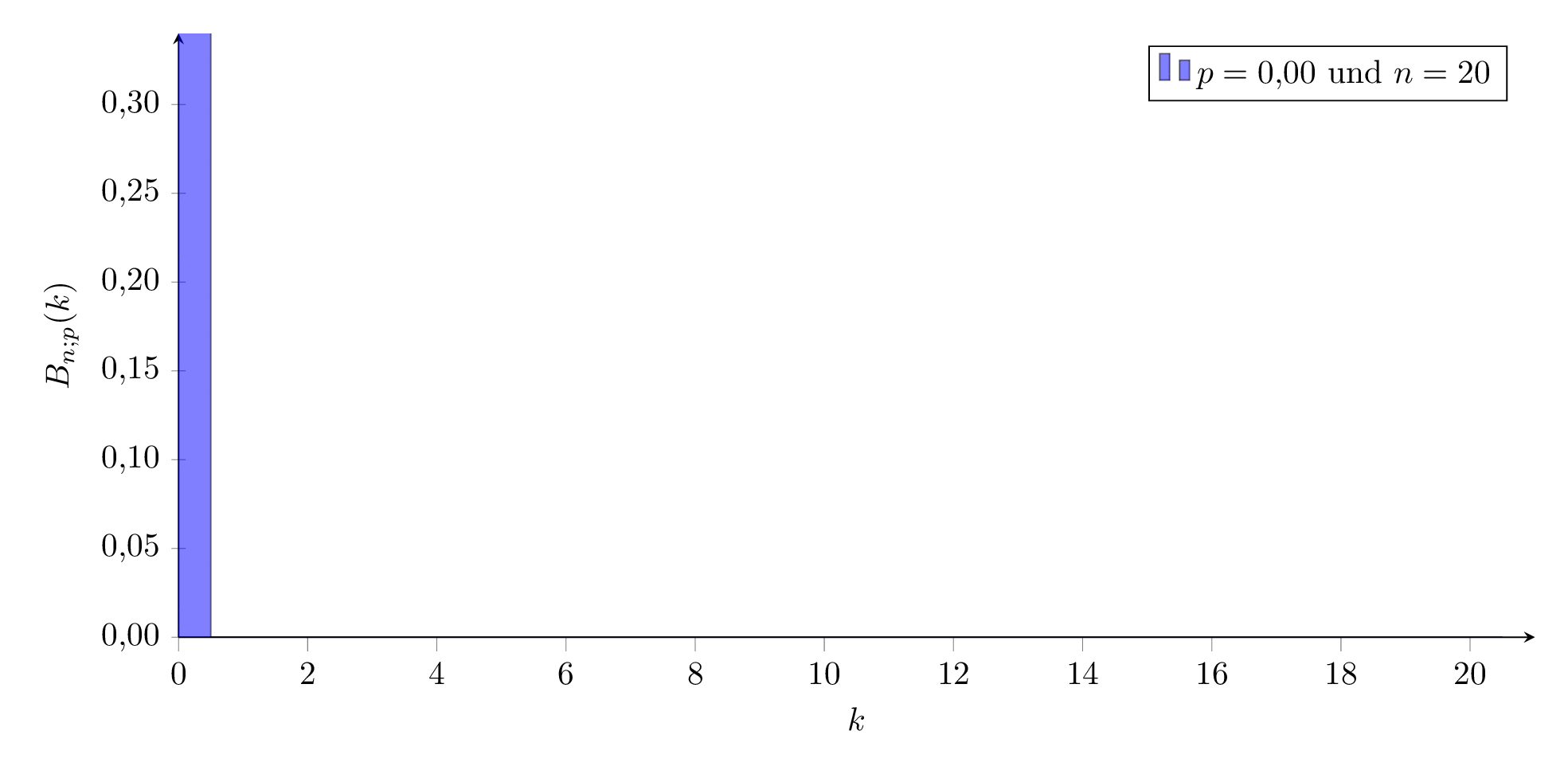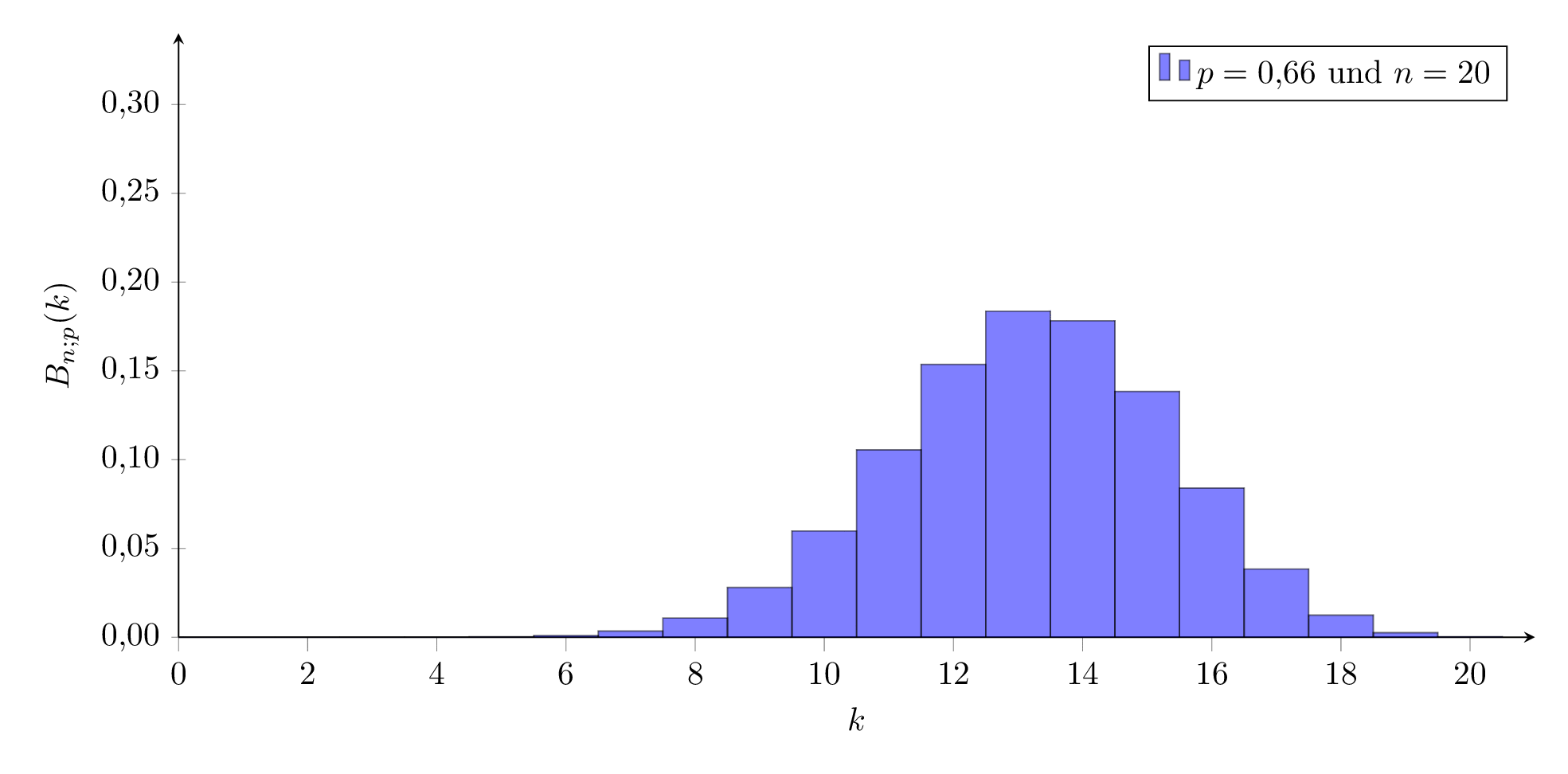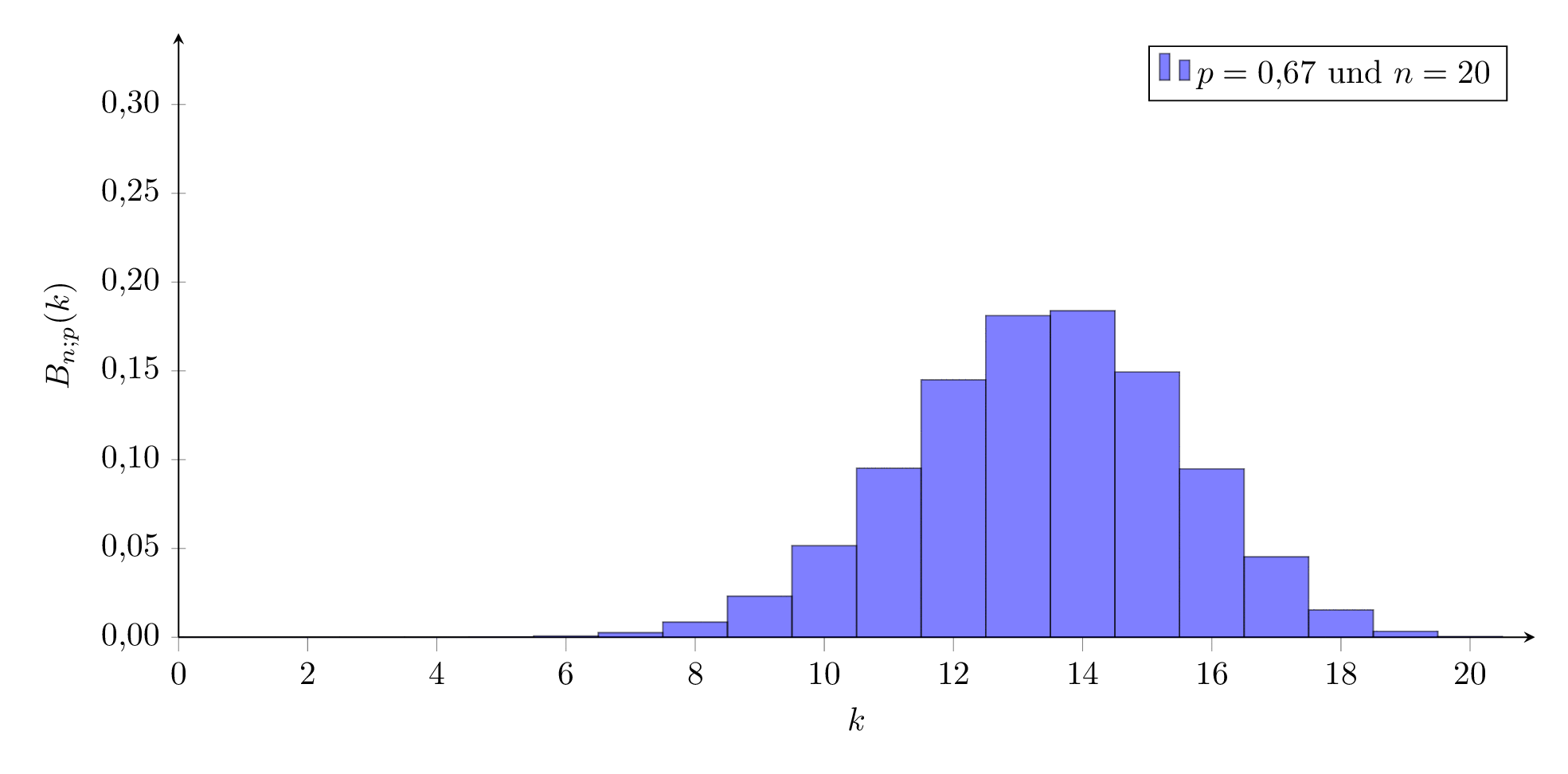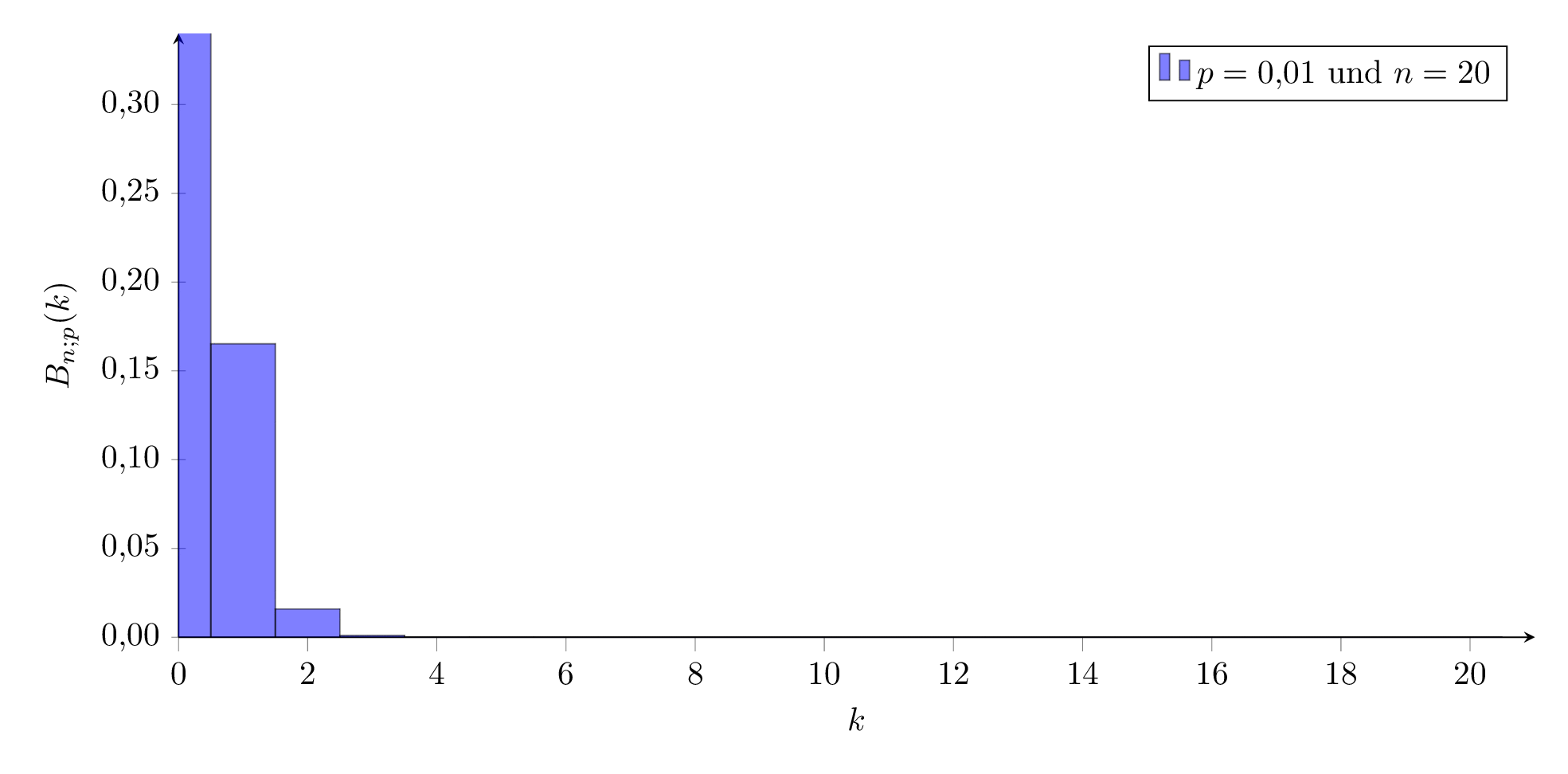
Für ein festes n verändert sich das Aussehen der Verteilung wie hier dargestellt:
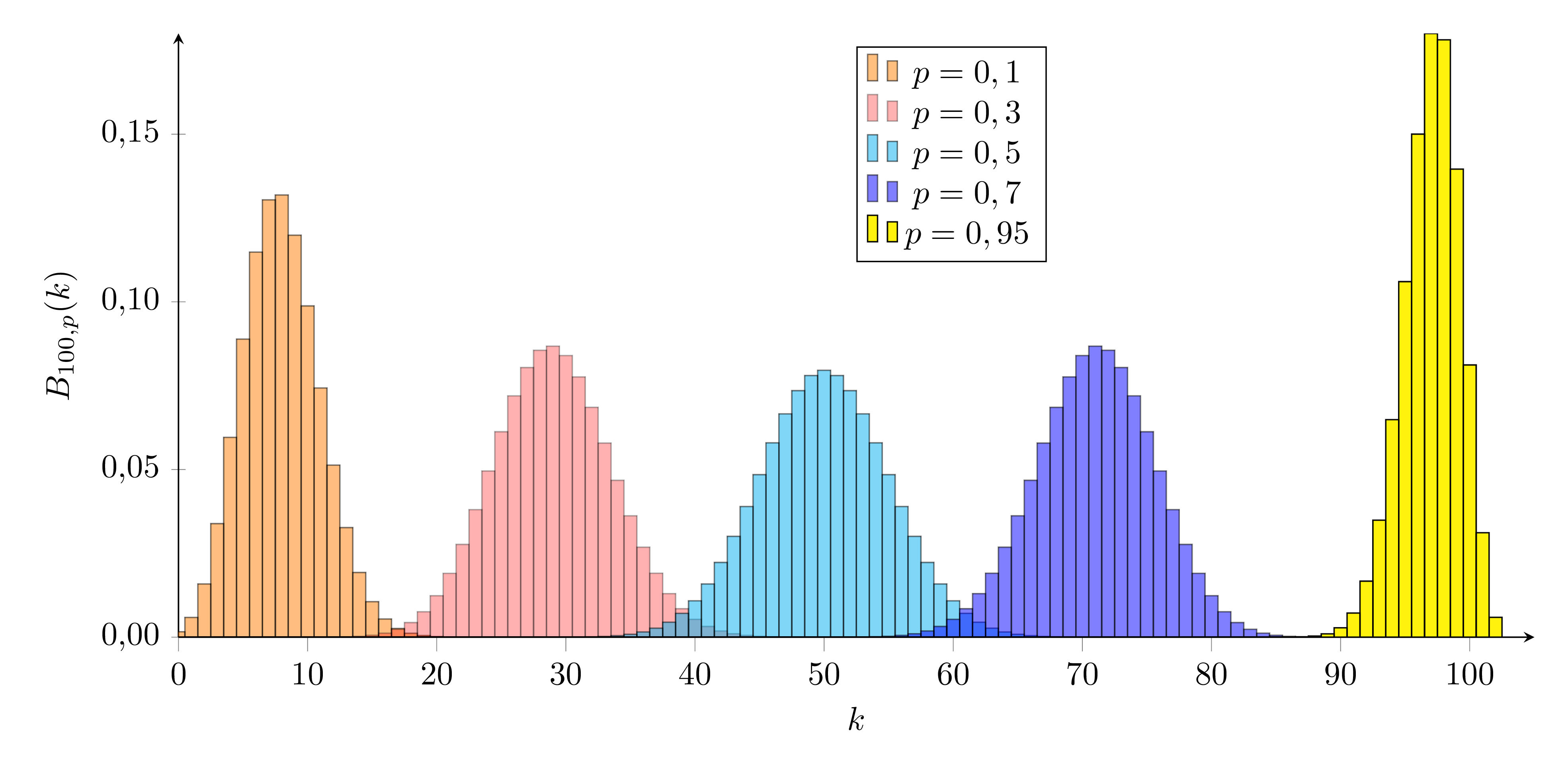 Für kleine und große Werte von p sieht sie ‘schief’ aus, für mittlere Werte sehr symmetrisch, ähnlich einer Welle, die von links nach rechts durch das Koordinatensystem wandert.
Für kleine und große Werte von p sieht sie ‘schief’ aus, für mittlere Werte sehr symmetrisch, ähnlich einer Welle, die von links nach rechts durch das Koordinatensystem wandert.
Dies kann natürlich auch dynamisch betrachtet werden:
Und hier mit n=100:
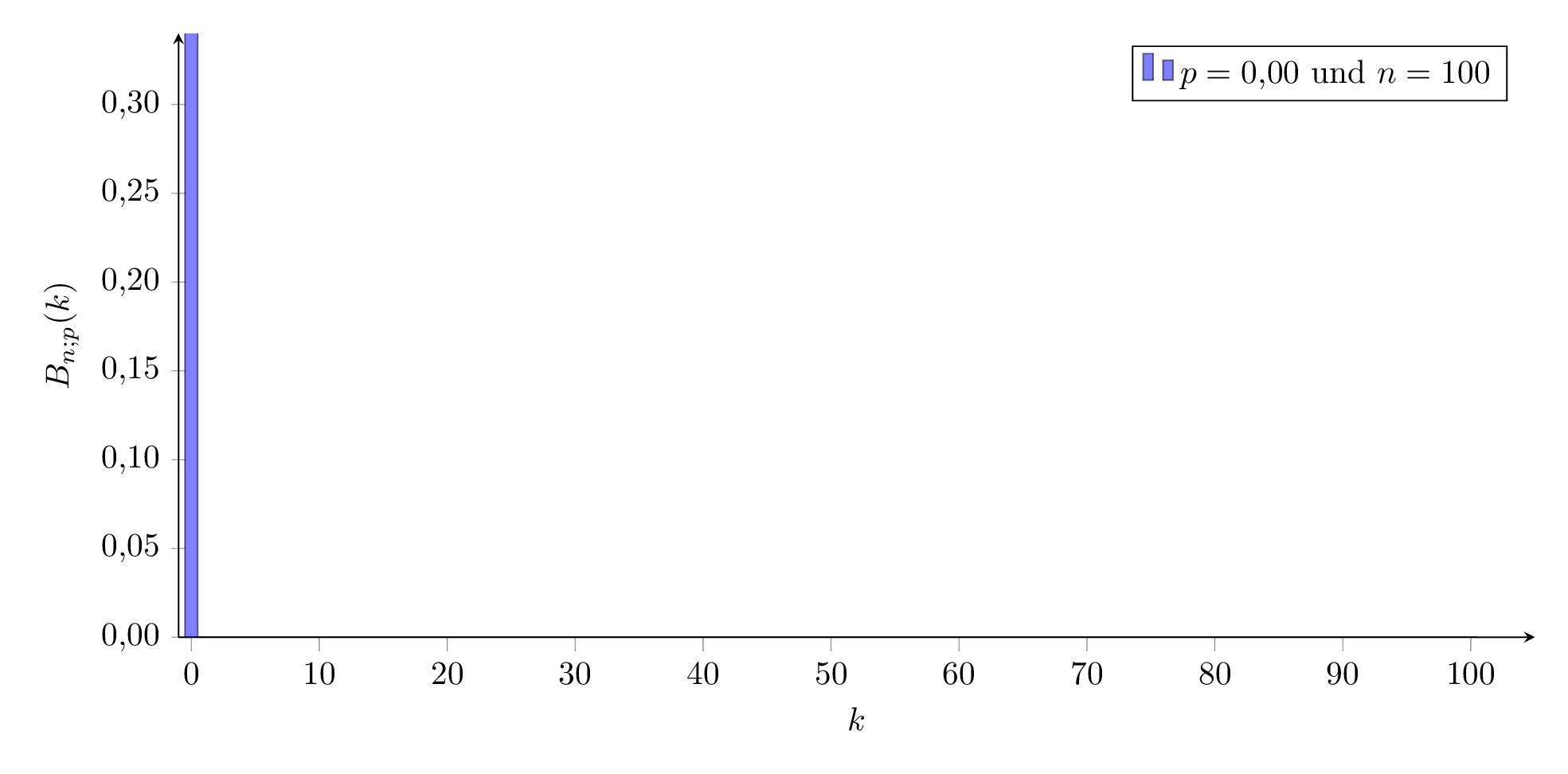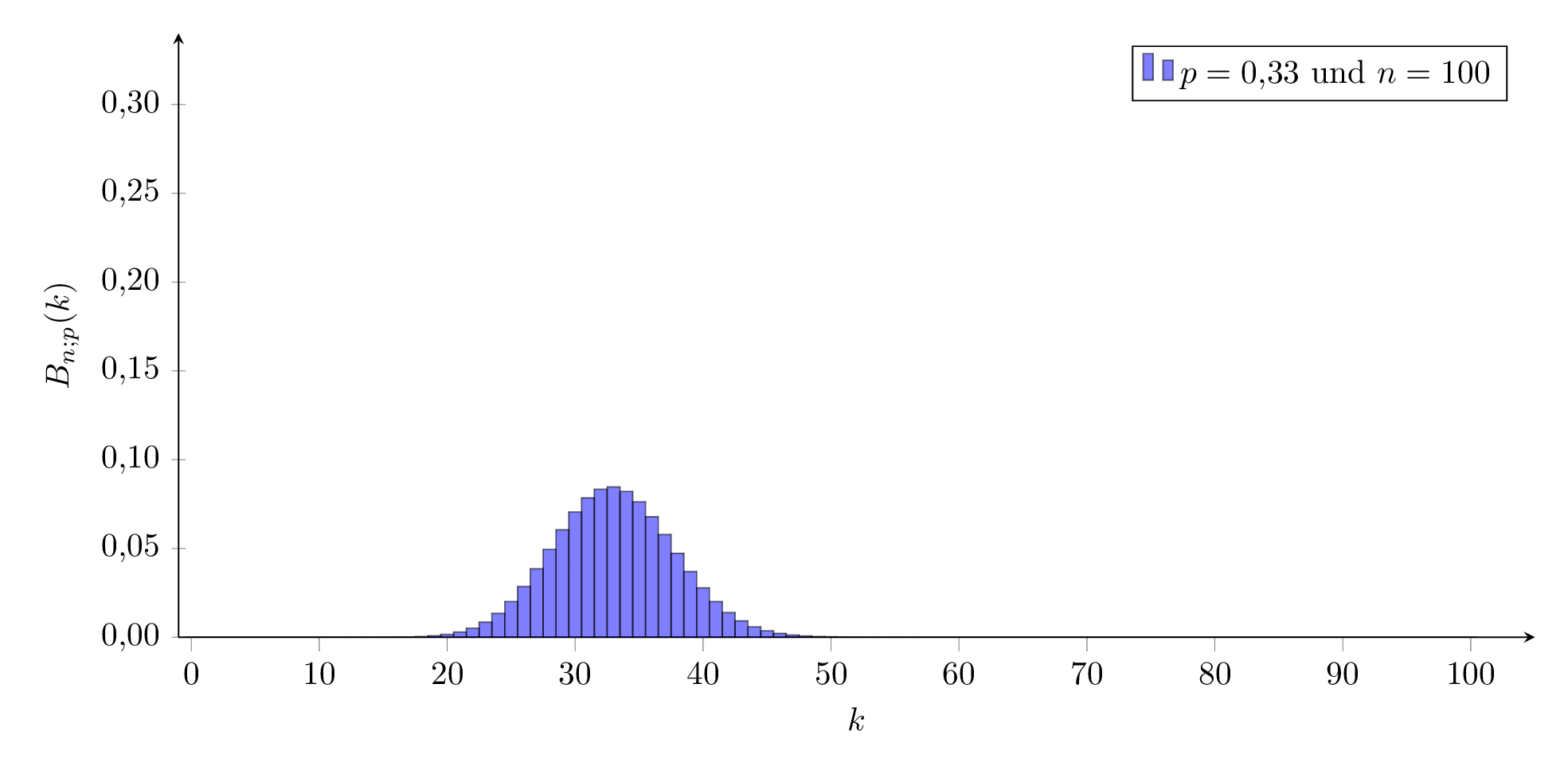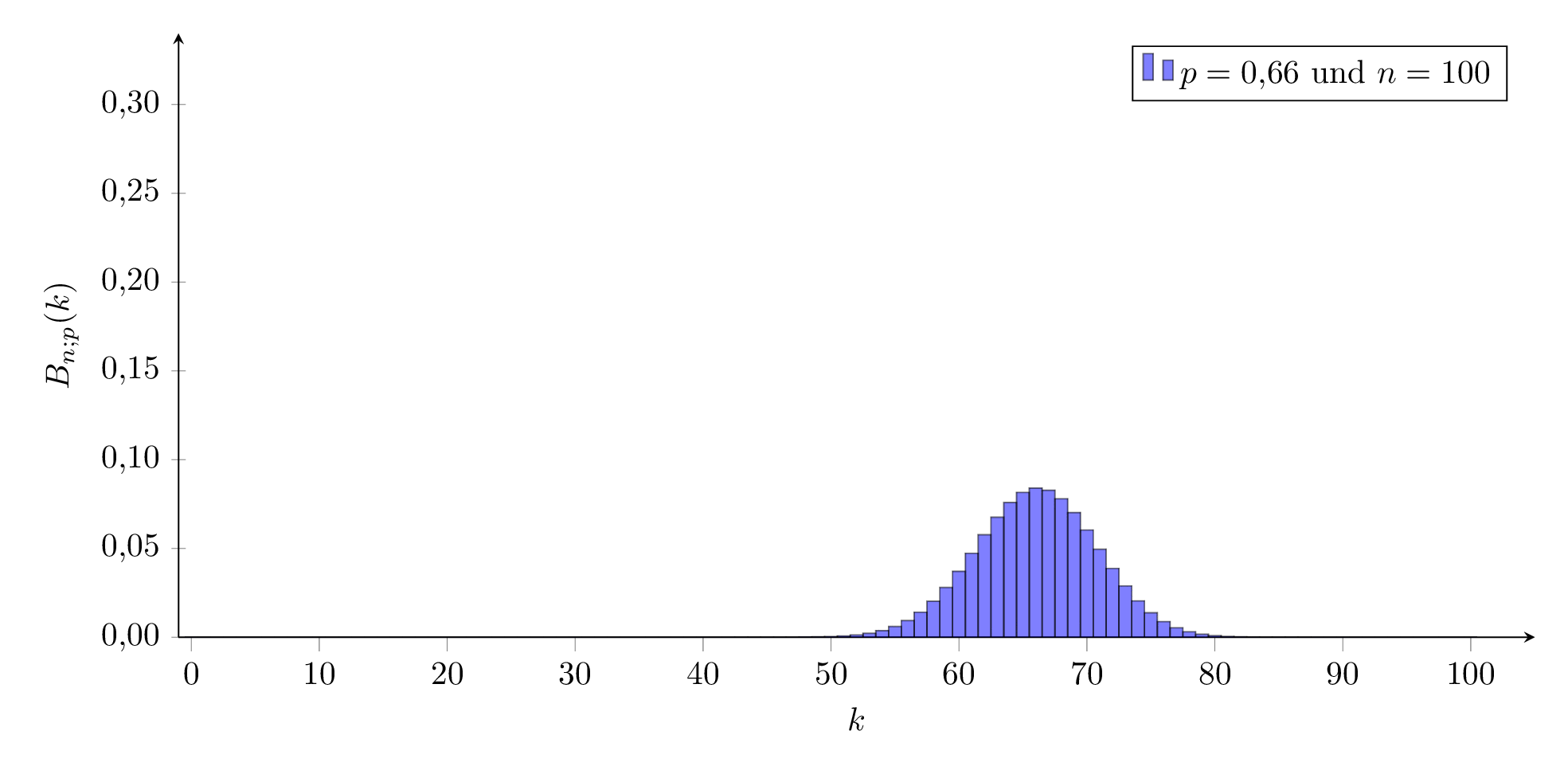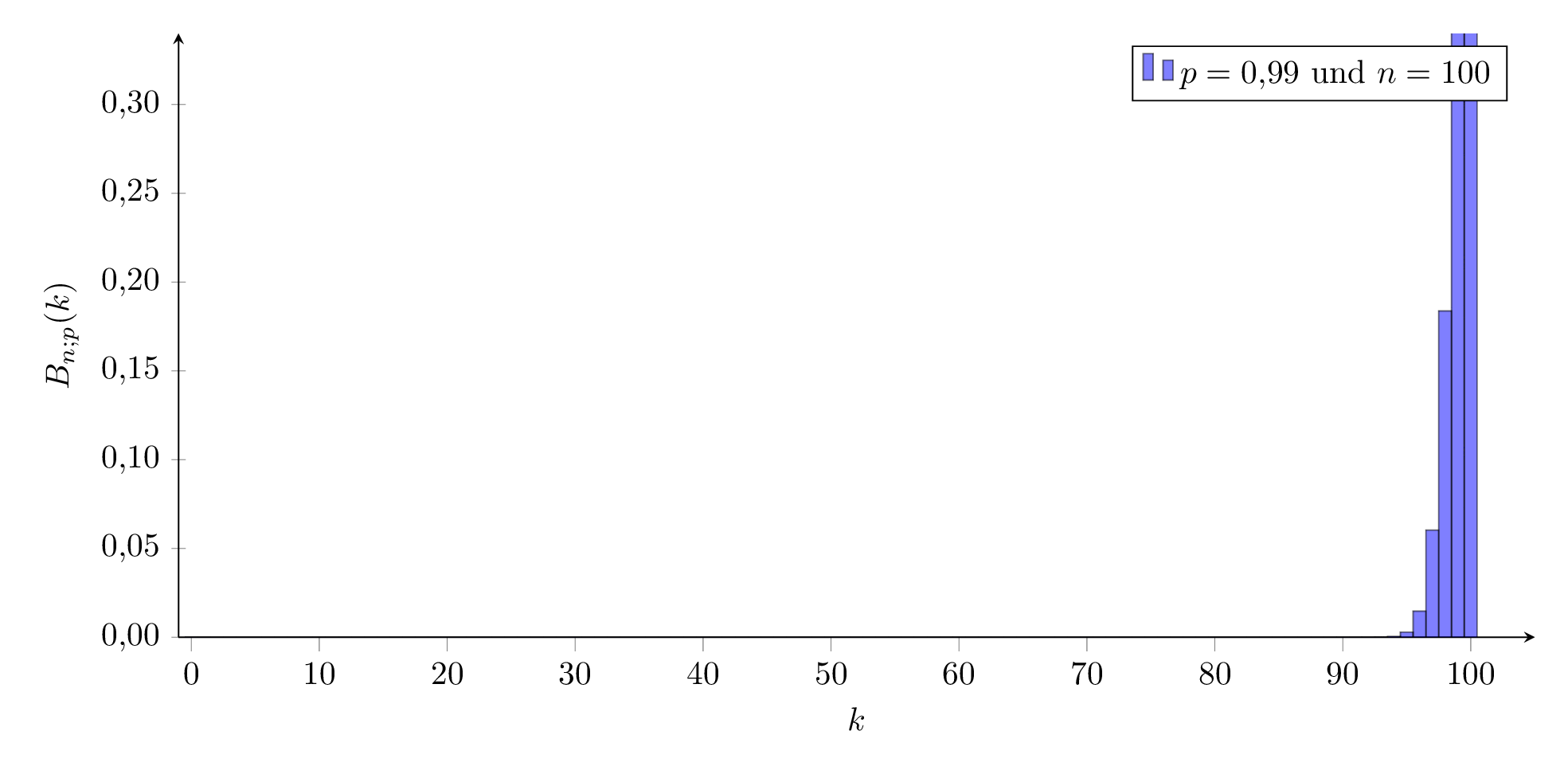
Aussehen der Binomialverteilung für verschiedene n:
Für immer größer werdendes n nähert sich die Binomialverteilung einer Glockenkurve an. Diese kann durch die Gauss’sche Normalverteilung dargestellt werden:
p=0,4 und n von 5 bis 100:
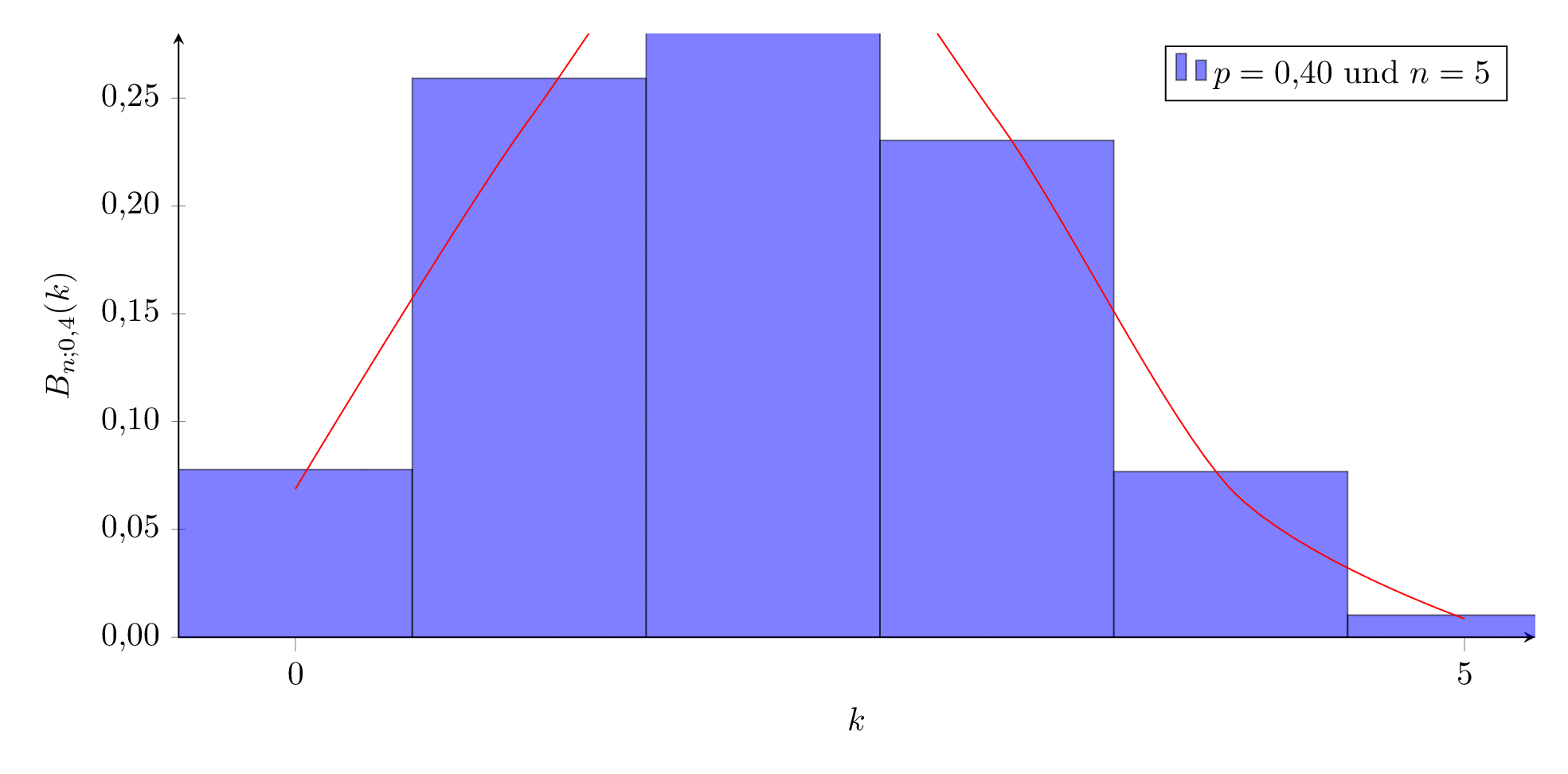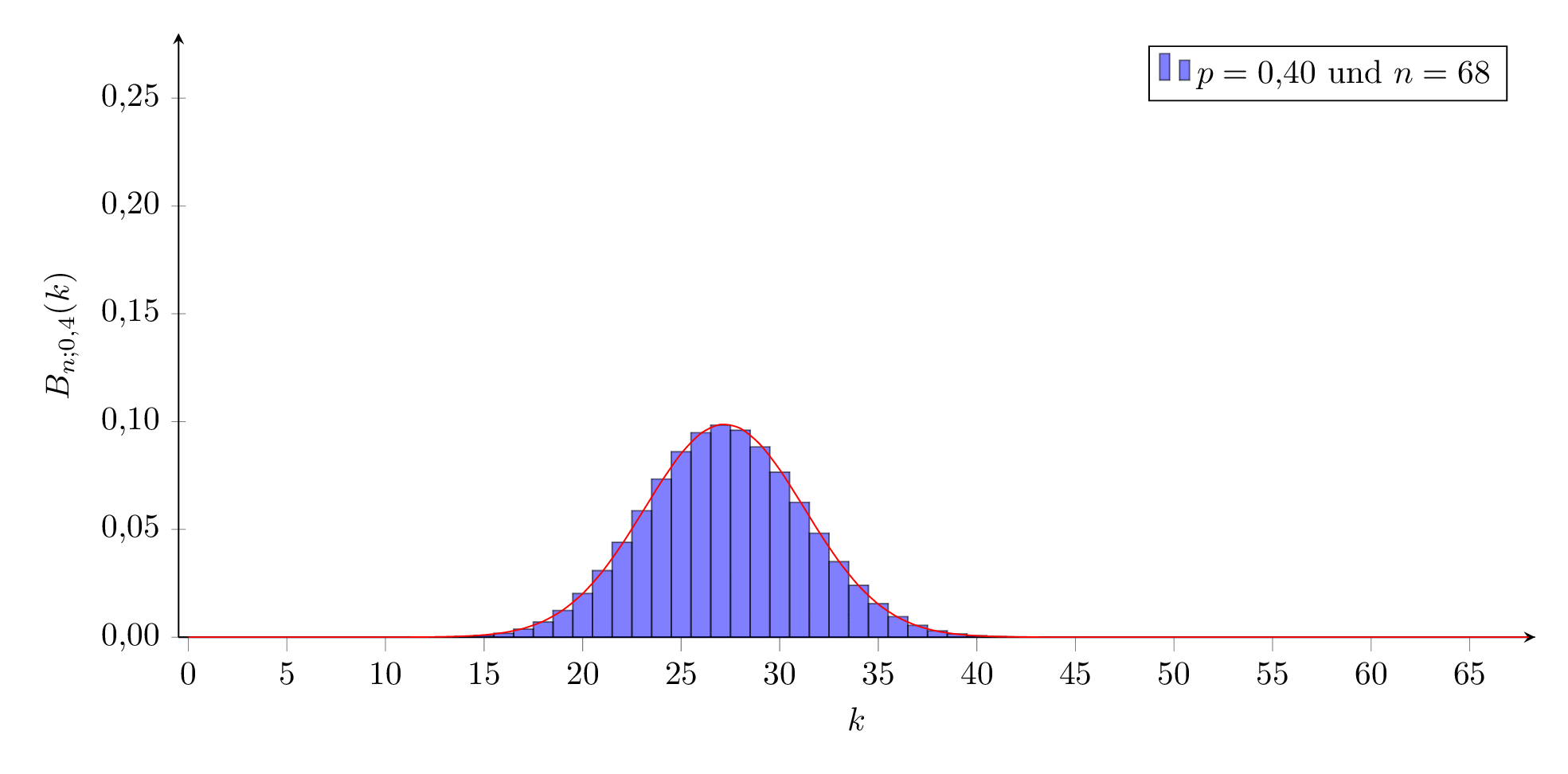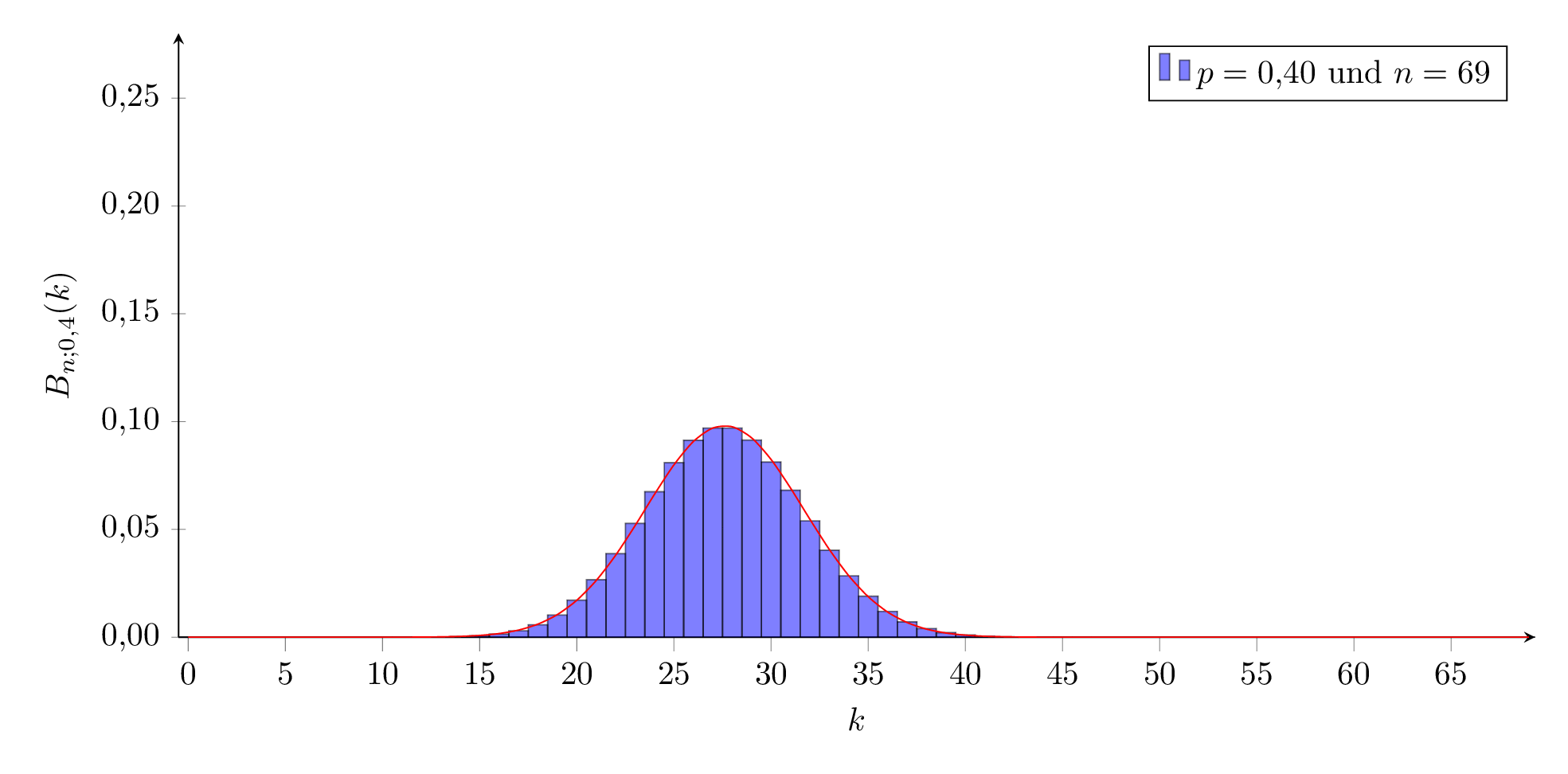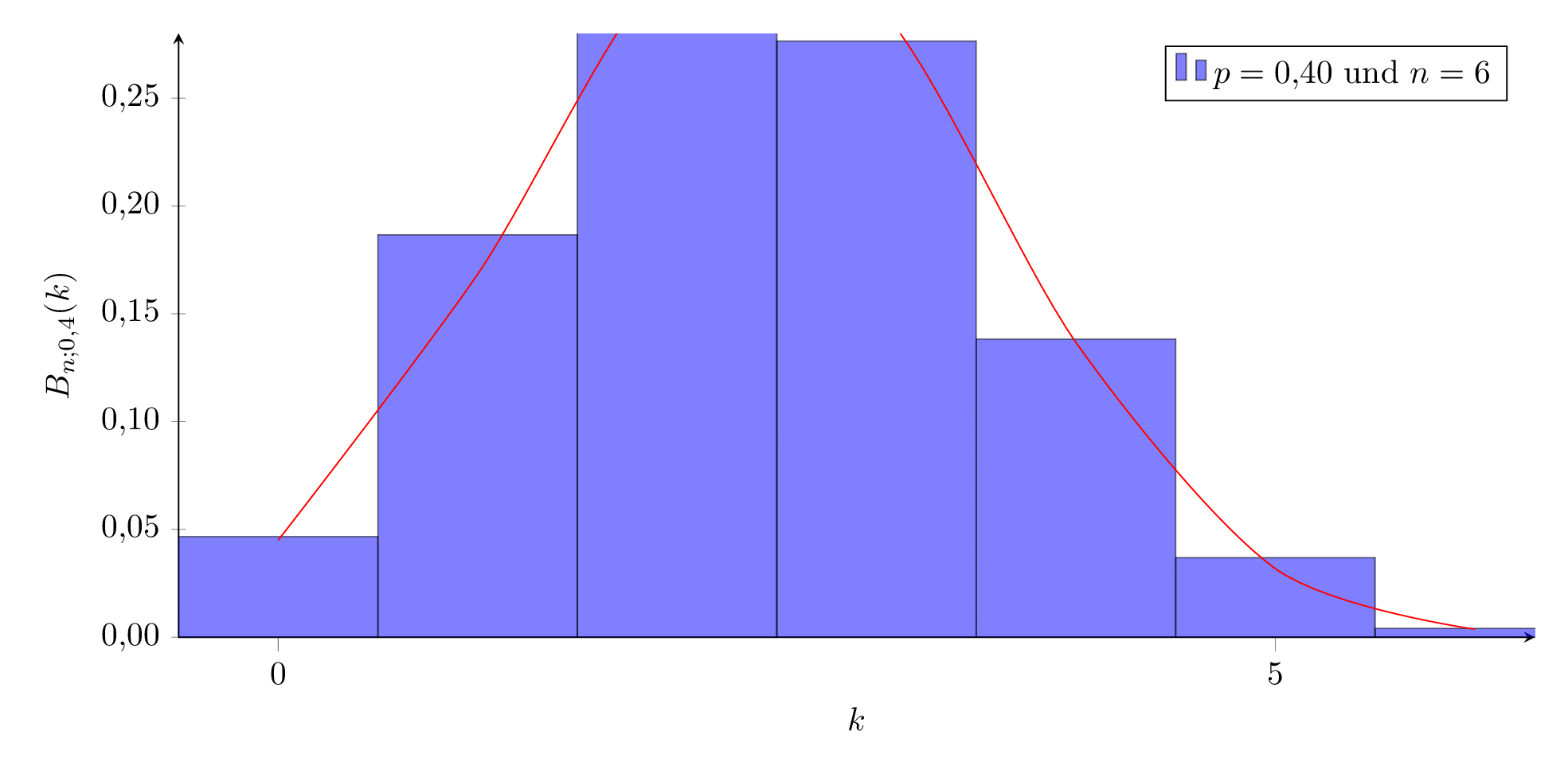
Die Sigma-Regeln
Hier kommen noch ein paar Erläuterungen udn Bildchen zu den Sigma-Regeln
28.04.2022
Das folgende Rätsel war angeblich unter GI’s (US-Soldaten) auf Guadalcanal (eine Insel im Pazifik) sehr beliebt:
Ein Mann besitzt ein Theater mit 100 Plätzen. Das Theater wird von 100 Zuschauern besucht. Die Eintrittspreise betragen 6 Cent für Männer, 2 Cent für Frauen und 1 Cent für je 10 Kinder.
Die Gesamteinnahmen betragen 1 Dollar.
Wie viele Frauen, Männer und Kinder besuchen das Theater?
Lösung:
Zunächst müssen die Variablen festgelegt werden.
Variablen festlegen:
\( x: \text{Anzahl Männer}\\
y: \text{Anzahl Frauen}\\
z: \text{Anzahl Kinder geteilt durch 10}\)
Die Anzahl der Kinder wird geschickterweise in Vielfache von 10 angegeben, damit im folgenden LGS die Zahlen nicht so groß werden bzw. nicht mit dem Bruch 101 gerechnet werden muss. 1 Dollar ist 100 Cent.
LGS aufstellen:
\[
\begin{align*} &\text{Besucherzahl:\quad} & x \;& + & y \;&+& 10z &= 100 \\
&\text{Einnahmen:} & 6x \;& + &2y \;&+& z &= 100 \end{align*}
\]
Das sind nur zwei Gleichungen für drei Unbekannte, das LGS ist also unterbestimmt. Da Personenzahlen aber nur ganzzahlig sein können und zudem zwischen 0 und 100 liegen müssen, kommen zu diesen Bedingungen noch welche hinzu, die nicht als Gleichungen ausdrückbar sind (man könnte sie holonome Bedingungen nennen).
Man löst das LGS zunächst soweit auf wie möglich und drückt die Anzahl Frauen und Männer in Abhängigkeit von z aus:
\[
\begin{align} & x \;& + & y \;&+& 10z &= 100 \\
& 6x \;& + &2y \;&+& z &= 100 \end{align}
\]

 Es gibt natürlich noch mehr Lösungsmöglichkeiten. Aber eine mit weniger als 5 zusätzlichen Würfeln habe ich nicht gefunden.
Es gibt natürlich noch mehr Lösungsmöglichkeiten. Aber eine mit weniger als 5 zusätzlichen Würfeln habe ich nicht gefunden.
 Grafisch bedeutet dies, dass der Schätzwert 373 gerade außerhalb des 97,5%-Bereichs der orangenen Verteilung und gerade unterhalb des 2,5%-Bereichs der blauen Verteilung liegt.
Grafisch bedeutet dies, dass der Schätzwert 373 gerade außerhalb des 97,5%-Bereichs der orangenen Verteilung und gerade unterhalb des 2,5%-Bereichs der blauen Verteilung liegt. Wir suchen also eine Binomialverteilung für die Untergrenze
Wir suchen also eine Binomialverteilung für die Untergrenze  Mit der Näherungsformel (deren Einsatz hier wegen der kleinen Zahl fragwürdig ist) ergibt sich für die Grenzen der Wahrscheinlichkeit
\[ \begin{align*} p_{o/u} &= h \pm c\cdot\sqrt{\frac{h(1-h)}{n}}\\[5pt]
p_{o/u} &= 0{,}360 \pm 1{,}96\cdot\sqrt{\frac{0{,}36(1-0{,}36)}{50}}\\[5pt]
p_{o/u} &\approx 0{,}360 \pm 0{,}133
\end{align*}\]
also
Mit der Näherungsformel (deren Einsatz hier wegen der kleinen Zahl fragwürdig ist) ergibt sich für die Grenzen der Wahrscheinlichkeit
\[ \begin{align*} p_{o/u} &= h \pm c\cdot\sqrt{\frac{h(1-h)}{n}}\\[5pt]
p_{o/u} &= 0{,}360 \pm 1{,}96\cdot\sqrt{\frac{0{,}36(1-0{,}36)}{50}}\\[5pt]
p_{o/u} &\approx 0{,}360 \pm 0{,}133
\end{align*}\]
also  Im schlimmsten Fall müssen wir also
\[ n \ge \frac{4\cdot c^2}{l^2}\cdot 0{,}25=\frac{c^2}{l^2}
\]
Personen fragen. Da wir eine 95 %-ige Sicherheit haben wollen ist
Im schlimmsten Fall müssen wir also
\[ n \ge \frac{4\cdot c^2}{l^2}\cdot 0{,}25=\frac{c^2}{l^2}
\]
Personen fragen. Da wir eine 95 %-ige Sicherheit haben wollen ist  Für kleine und große Werte von
Für kleine und große Werte von 


 Von diesem Punkt aus markiert man einen weiteren Punkt auf der Kreislinie, der als Abstand einen Kreisradius vom ersten Punkt hat.
Von diesem Punkt aus markiert man einen weiteren Punkt auf der Kreislinie, der als Abstand einen Kreisradius vom ersten Punkt hat.
 Von diesem Punkt aus markiert man den nächsten Punkt auf die selbe Art. Dieses Verfahren setzt man fort, bis man wieder beim Ausgangspunkt angekommen ist.
Von diesem Punkt aus markiert man den nächsten Punkt auf die selbe Art. Dieses Verfahren setzt man fort, bis man wieder beim Ausgangspunkt angekommen ist.
 Verbindet man nun die markierten Punkte, so erhält man ein regelmäßiges Sechseck mit der gewünschten Seitenlänge:
Verbindet man nun die markierten Punkte, so erhält man ein regelmäßiges Sechseck mit der gewünschten Seitenlänge:
 Da in einem regelmäßigen Sechseck jeder Innenwinkel 120° weit ist, wird es durch drei Diagonalen in sechs gleichseitige Dreiecke zerlegt (in gleichseitigen Dreiecken ist jeder Innenwinkel 60° weit). Diese Eigenschaft wurde bei dieser Konstruktion genutzt.
Da in einem regelmäßigen Sechseck jeder Innenwinkel 120° weit ist, wird es durch drei Diagonalen in sechs gleichseitige Dreiecke zerlegt (in gleichseitigen Dreiecken ist jeder Innenwinkel 60° weit). Diese Eigenschaft wurde bei dieser Konstruktion genutzt.
