Die natürliche Exponentialfunktion

Eine besondere Exponentialfunktion

Für welche Basis $b$ ist die Parallele zur ersten Winkelhalbierenen $y=x+1$ Tangente am Schaubild $K$ einer Exponentialfunktion 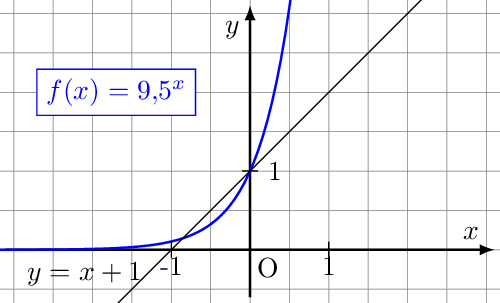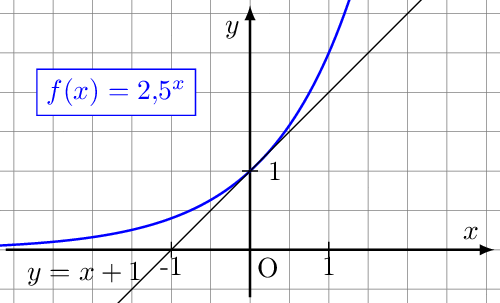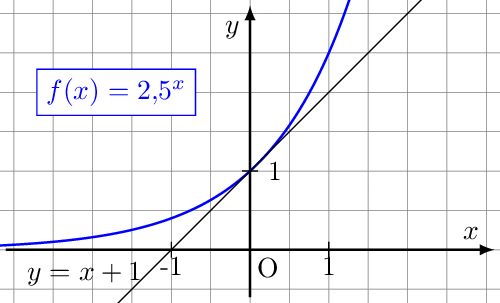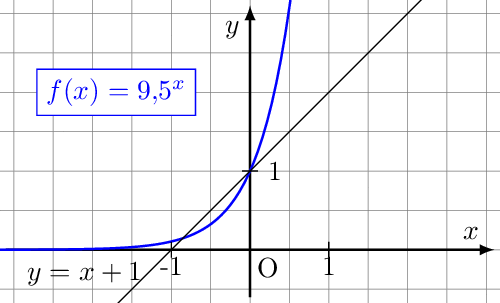$f(x)=b^x$ im Punkt $(0|1)$? Alle Exponentialfunktionen haben mit der Geraden den Punkt $(0|1)$ gemeinsam. Ist $b$ zu groß, dann erkennt man einen zweiten gemeinsamen Punkt im zweiten Quadranten, der immer näher an $(0|1)$ heranrückt, je kleiner $b$ wird. Ist $b$ kleiner als etwa 2,7 befindet sich der zweite gemeinsame im ersten Quadranten und rückt weiter nach rechts, je kleiner $b$ wird. Es muss also einen Wert etwa zwischen 2,0 und 3,5 geben, für den die beiden gemeinsamen Punkte zu einem verschmelzen. Das ist die gesuchte Basis.
Das ist dann der Fall, wenn das Schaubild $K$ nie unterhalb der Gerade verläuft. Es muss also gelten: \[ b^x \ge x+1\] Wir ziehen die $x$-te Wurzel auf beiden Seiten (da wir positive Werte suchen sollte das kein Problem sein) und erhalten \[ b \ge \sqrt[x]{x+1}\] Das kann man mit den Potenzregeln auch so schreiben: \[ b \ge (x+1)^{\frac{1}{x}}\] Die Gleichheit sollte gelten, wenn $x=0$ ist, also im Punkt $(0|1)$. Allerdings müssten wir dann durch Null dividieren, was aber nicht geht…
Wir können uns der Null aber annähern: \[ b = \lim_{x\rightarrow 0} (x+1)^{\frac{1}{x}}\] Uns stört der Bruch. Substituieren wir doch einfach mal $x$ durch $\frac{1}{n}$ also \[ x=\frac{1}{n}\quad \text{bzw.} \quad n = \frac{1}{x}\] Wenn $x\rightarrow 0$ gegen Null geht, dann geht $n\rightarrow \infty$ gegen Unendlich und wir erhalten \[ b = \lim_{n\rightarrow \infty} (1+\frac{1}{n})^{n} = \text{e} \quad \color{red}{\text{!!!}}\] Das ist gerade die Definition der Eulerschen Zahl $\text{e}$!

Das Schaubild der Funktion $f$ mit $f(x)=\text{e}^x$ hat im Punkt $(0|1)$ eine Tangente, die parallel zur ersten Winkelhalbierenden ist.
Die Exponentialfunktion mit der Eulerschen Zahl $\text{e}$ als Basis ist diejenige Exponentialfunktion, die an der Stelle $x=0$ die Steigung 1 hat!

Die Funktion \[ f: x\rightarrow \text{e}^x \] ($\text{e}$: Eulersche Zahl)
heißt Natürliche Exponentialfunktion. Sie spielt eine herausragende Rolle in Naturwissenschaften und Technik (und im Rest der Welt natürlich auch).