Optimierungsaufgabe Tunnel

Hier ist die Lösung:

Variable festlegen:

Als Variable wählen wir die halbe Deckenbreite $u$ in Meter (siehe Zeichnung) mit $0 \le u \le 4$.

Nebenbedingungen formulieren:

Die zu optimierende Größe ist der Flächeninhalt eines Trapezes. Zur Berechnung des Flächeninhalts $(A_{\text{Trapez}}=\frac{a+c}{2}\cdot h)$ brauchen wir die Höhe und die zwei dazugehörigen Seitenlängen:
$a=8$
$c=2\cdot u$
$h=f(u)=-\frac{1}{4}u^2+4$ (der rechte obere Eckpunkt liegt auf der Parabel).

Zielfunktion aufstellen:

Der Flächeninhalt $A$ des Trapezes soll maximal werden:
$A=\frac{a+c}{2}\cdot h$
Alles einsetzen:
$A(u)=\frac{8+2u}{2}\cdot f(u) = (4+u)\cdot (-\frac{1}{4}u^2+4)$
$A(u)=-\frac{1}{4}u^3-u^2+4u+16$

Optimierung der Zielfunktion:

Die Zielfunktion ist keine quadratische Funktion, sie kann also nicht mit Methoden der Eingangsklasse optimiert werden. Daher muss das numerisch (mit dem Taschenrechner) gemacht werden:

$u$ wird in Meter angegeben, eine sinnvolle Genauigkeit des Ergebnisses wäre Zentimeter. Daher wird $u$ auf 2 Nachkommastellen genau durchprobiert. Gib den Wert vor dem Optimium und den Wert nach dem Optimium an.

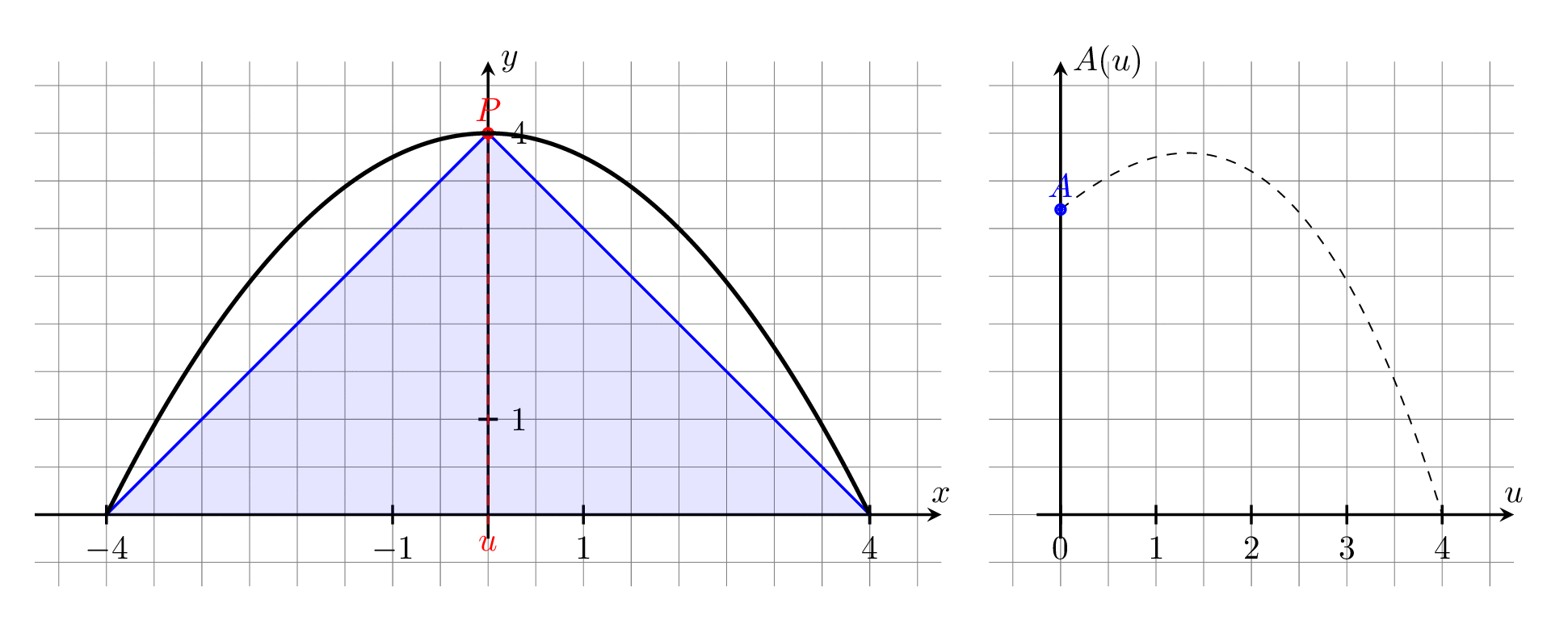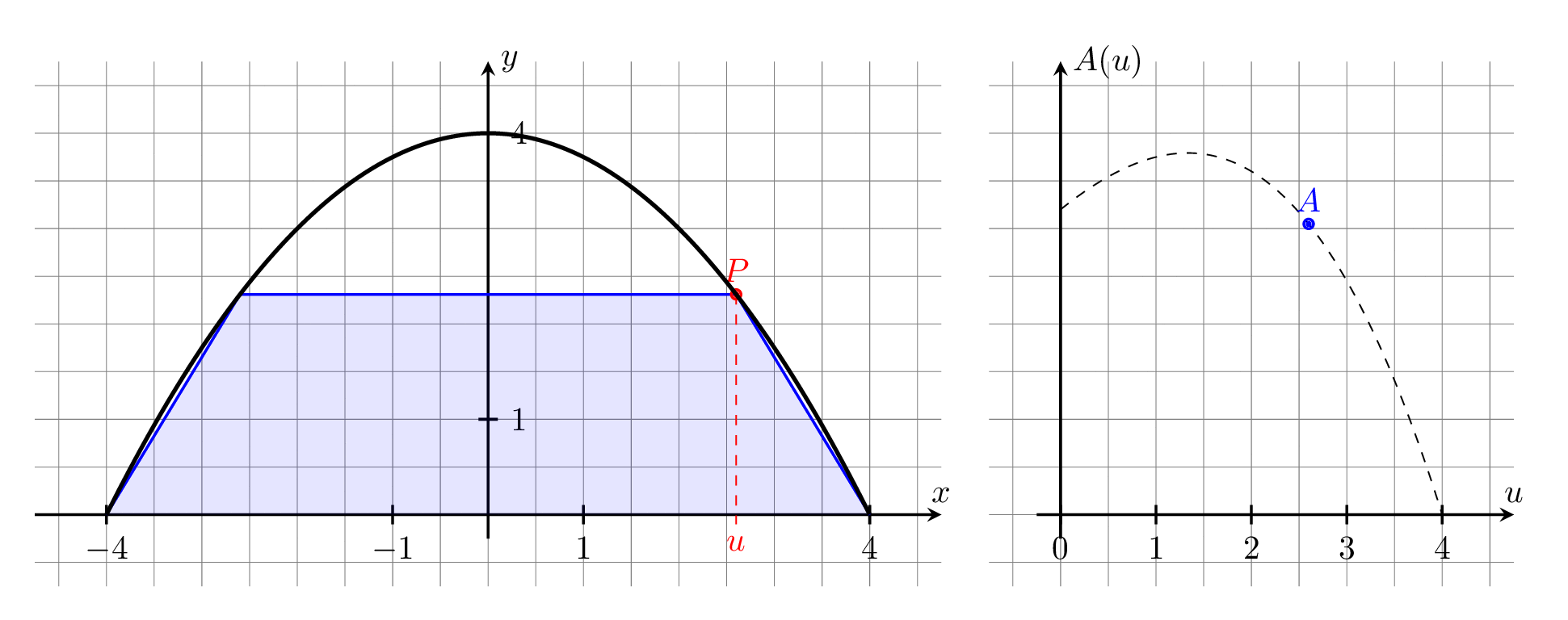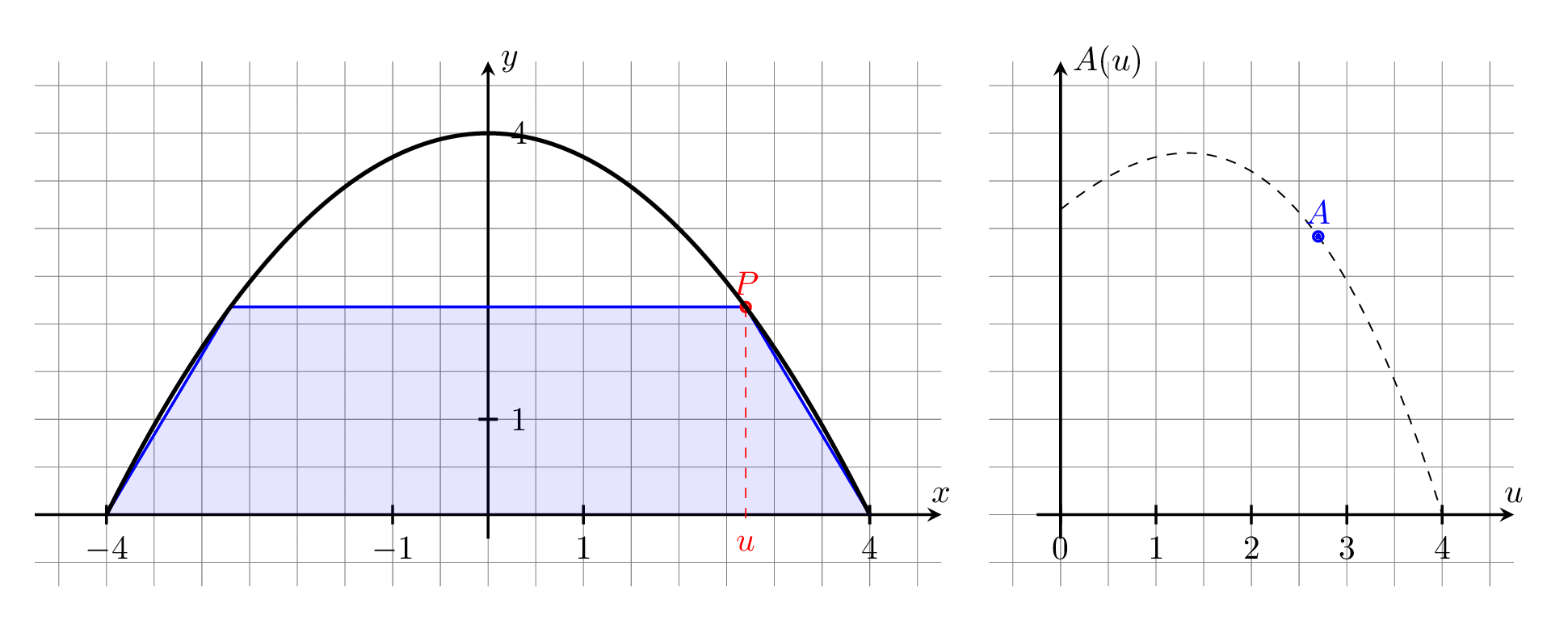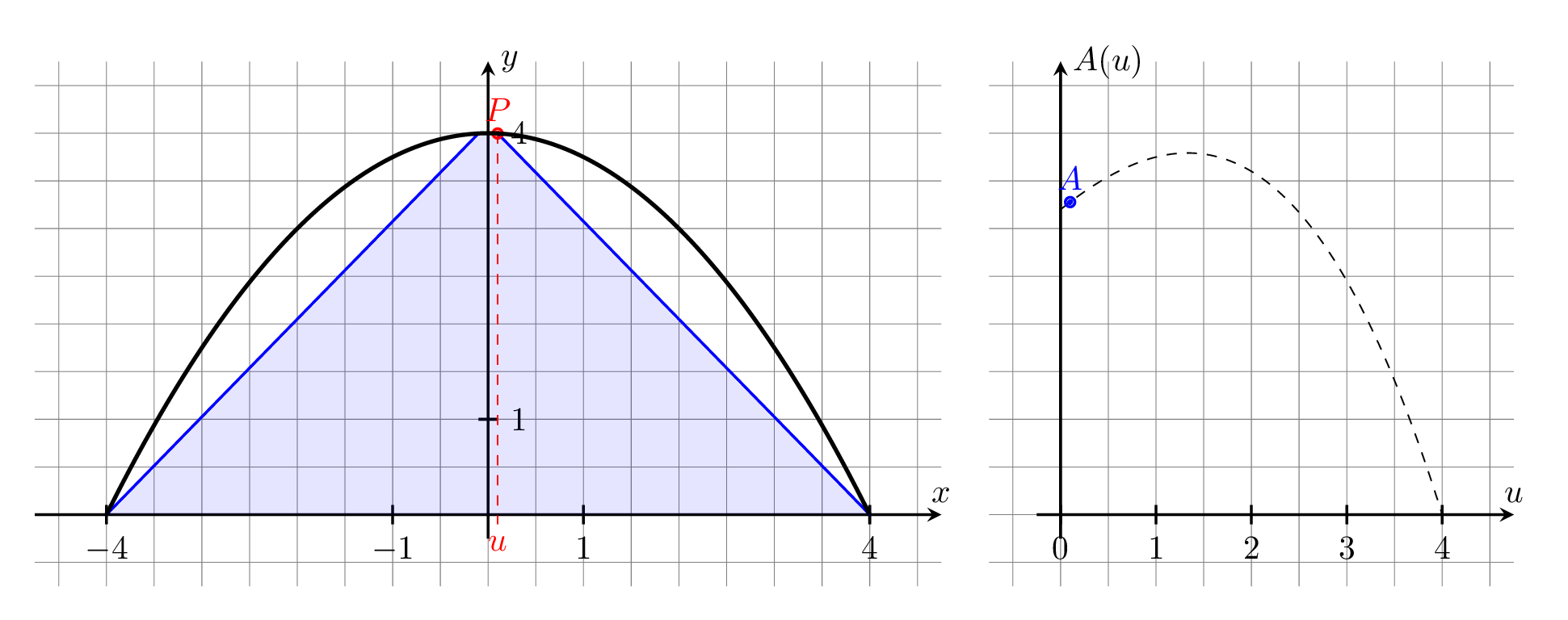
Randwertbetrachtung:

Bitte nicht vergessen und gleich angewöhnen!
$A(0)=16 < 18,96$
$A(4)=0$
Kein Randextremum.

Interpretation im Sachzusammenhang:

$h=f(1,33)=-0,25 \cdot 1,33^2+4\approx 3,56$
Die größtmögliche trapezförmige Querschnittsfläche ist $3,56\; \text{m}$ hoch, hat eine Deckenbreite von $2 \cdot 1,33\; \text{m} = 2,66\; \text{m}$ und eine Querschnittsfläche von ca. $18,96 \;\text{m}^2$.