Johnnys Tafel Ansichten eines Lehrers

Vertrauensintervalle (Konfidenzintervalle)

16.10.2022

Einstiegsbeispiel: Wahlergebnis

Für die Kommunalwahl am kommenden Sonntag hat eine kandidierende Partei eine Umfrage durchgeführt. Dabei wurden 1000 Personen befragt und 373 gaben an, diese Partei zu wählen. Die Frage ist, mit wie viel Prozent der Stimmen die Partei bei der Wahl rechnen kann. Als wahrscheinlichsten Wert würde man 37,3  %37{,}3 \;\% annehmen, da dies genau der relativen Häufigkeit hh aus der Umfrage entspricht. (Dies nennt man eine Punktschätzung ) Genauer betrachtet sucht man eine unbekannte Wahrscheinlichkeit pp, hier das Wahlergebnis am Sonntag. In der Praxis gibt man gerne ein Intervall an, in dem der Schätzwert (hier das Umfrageergebnis) mit hoher Wahrscheinlichkeit liegt, ein sogenanntes Vertrauensintervall oder auch Konfidenzintervall genannt. Ein gängiger Wert ist das 95%-Vertrauensintervall , das Intervall für pp, in dem der Schätzwert mit 95  %95\;\%-iger Wahrscheinlichkeit liegt.

Die Sigma-Regel sagt uns, dass die beobachtete Trefferzahl (hier 373) mit 95%-iger Wahrscheinlichkeit im Intervall \[ [ \mu - 1{,}96 \cdot\sigma \quad; \quad\mu + 1{,}96 \cdot\sigma ] \] liegt. Durch einige Umformungen und Näherungen, die ich später einfügen werde, erhält man als Näherungswert für das Vertrauensintervall: \[ \tiny h - 1{,}96\cdot\sqrt{\frac{h\cdot(1-h)}{n}} \quad \le \quad p \quad \le \quad h + 1{,}96\cdot\sqrt{\frac{h\cdot(1-h)}{n}} \] Für das Beispiel ergibt sich somit, dass die Partei bei der Wahl am Sonntag mit einer Wahrscheinlichkeit von 95% zwischen 34,3% und 40,3% erhält. 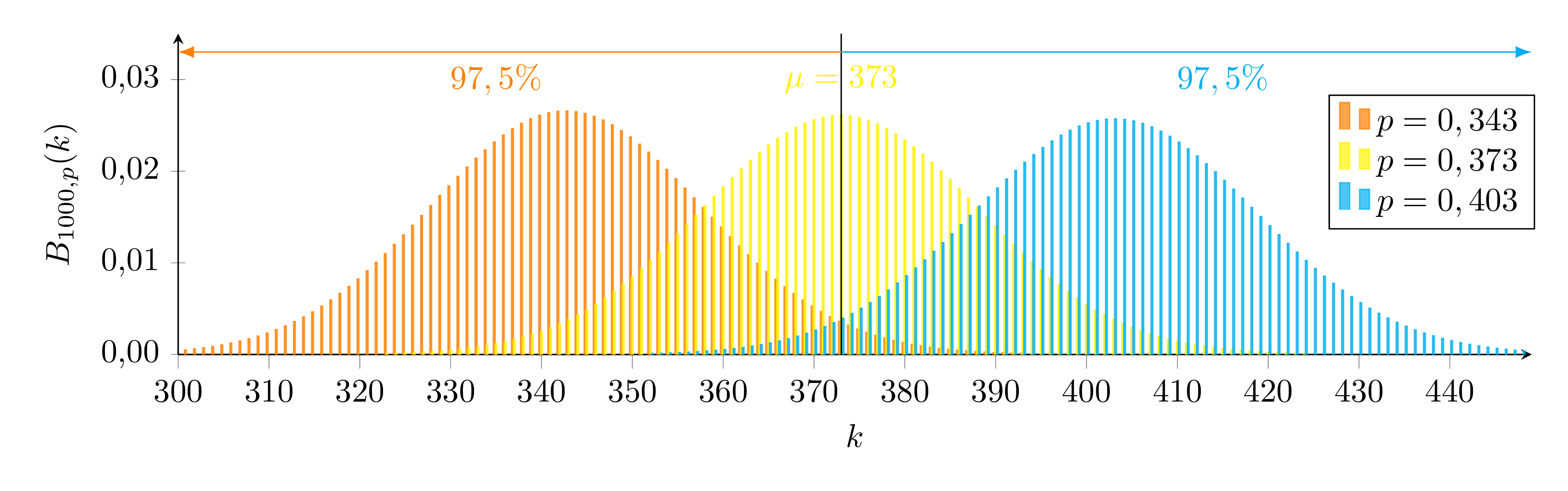Binomialverteilungen für die Intervallgrenzen und für h. Grafisch bedeutet dies, dass der Schätzwert 373 gerade außerhalb des 97,5%-Bereichs der orangenen Verteilung und gerade unterhalb des 2,5%-Bereichs der blauen Verteilung liegt.

Exakt bestimmen kann man dieses Intervall so:

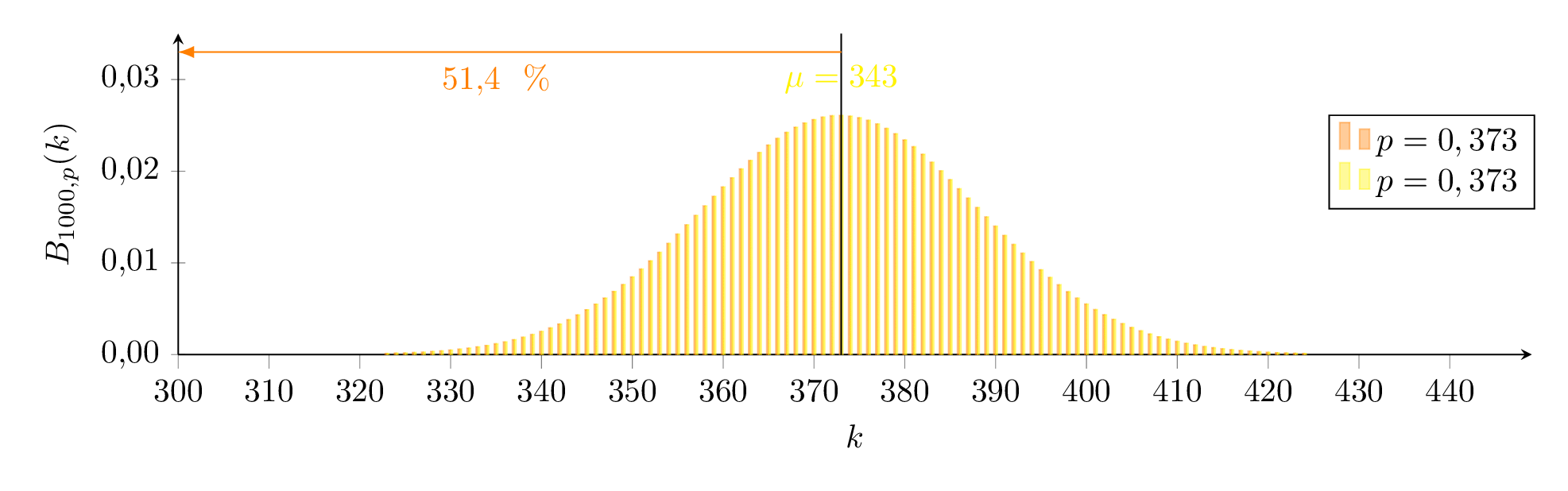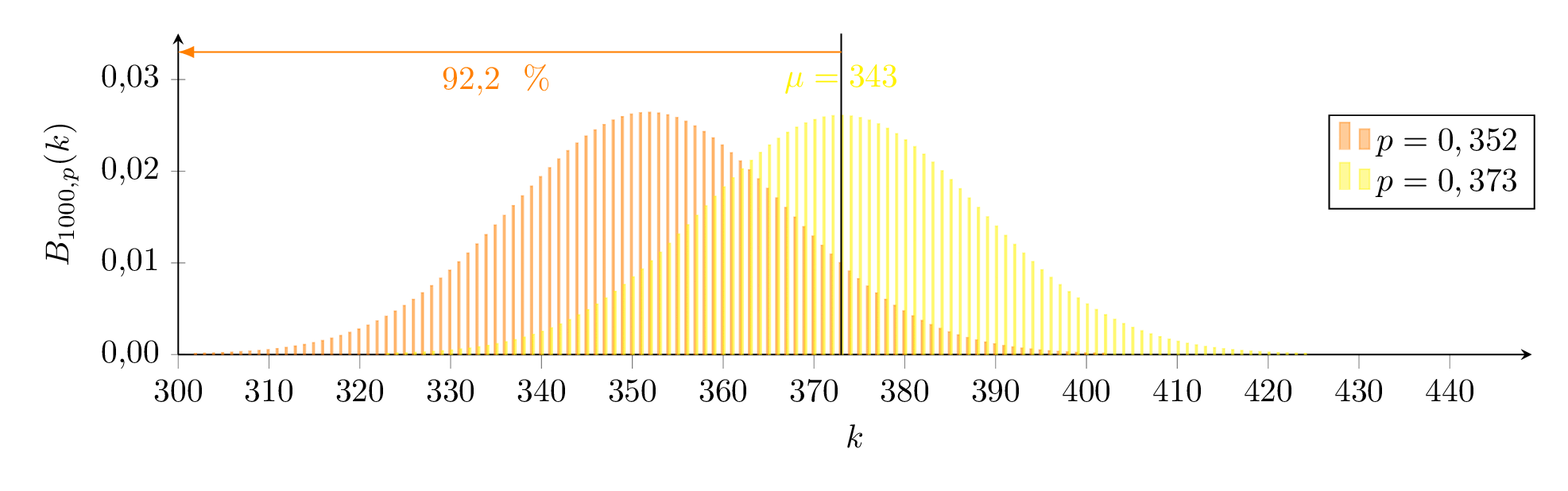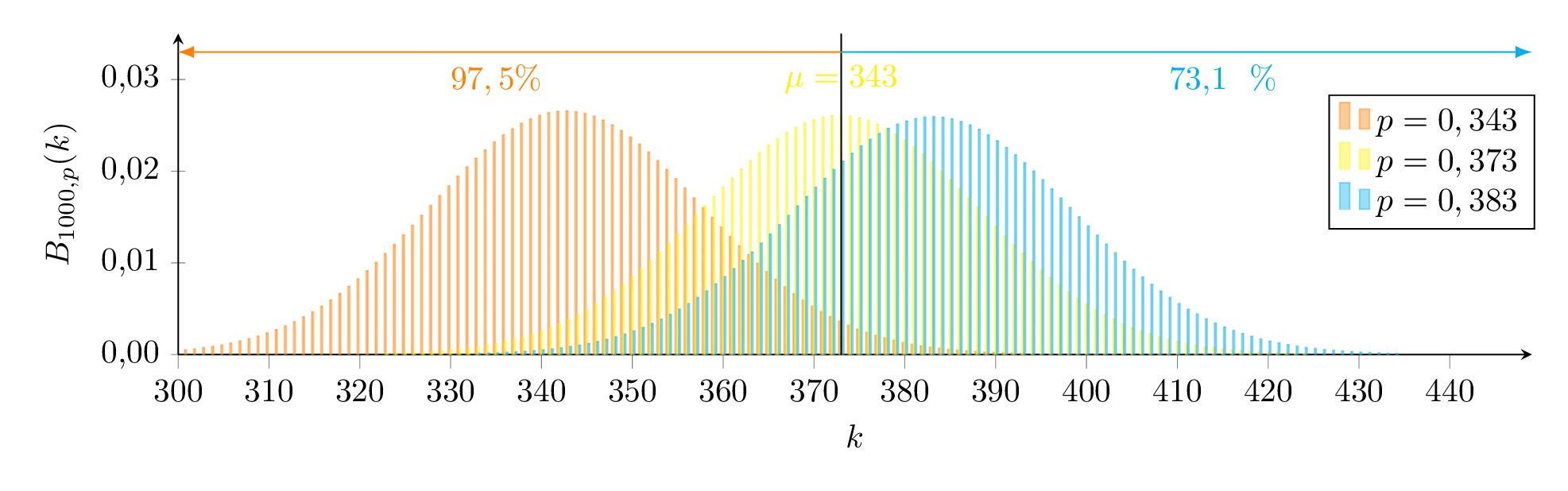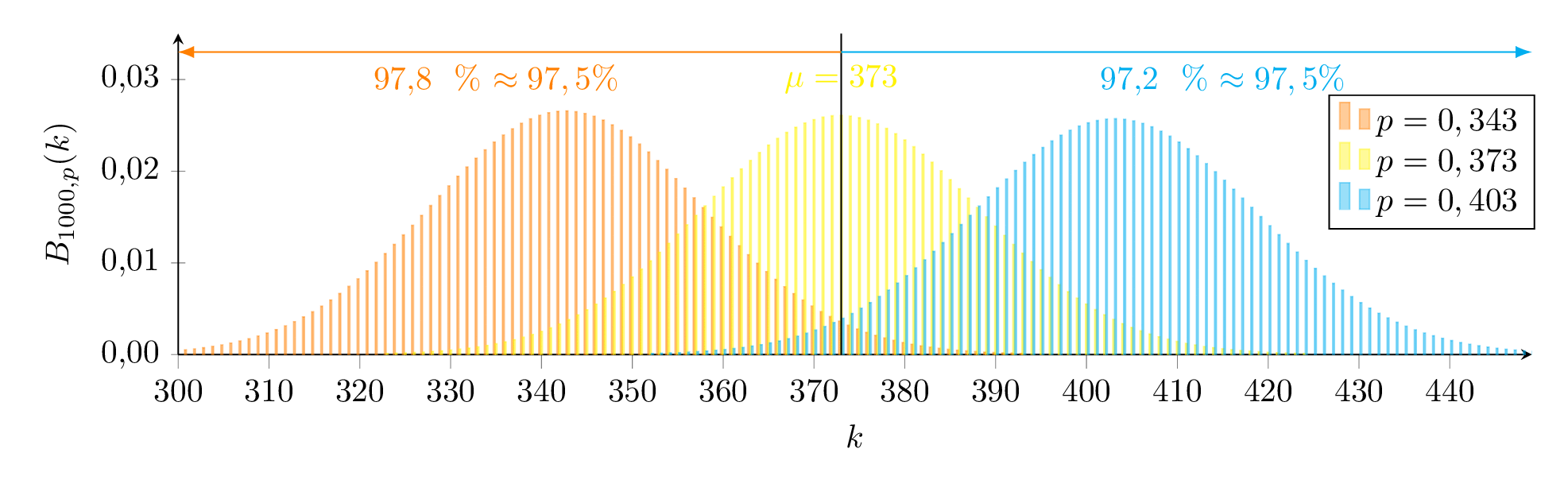Idee der Vertrauensintervall als Animation. Wir suchen also eine Binomialverteilung für die Untergrenze p1p_1 (orange) so, dass B1000;p1(X≤373)≥97,5B_{1000; p_1}(X\le 373) \ge 97{,}5% gilt und eine für die Obergrenze p2p_2 (blau) so, dass B1000;p2(X≥373)≥97,5B_{1000; p_2}(X\ge 373) \ge 97{,}5% gilt. Da man die Formel für die kummulierte Wahrscheinlichkeit bei der Binomialverteilung nicht nach pp auflösen kann, muss man sich mit dem Taschenrechner (oder dem Computer) durch gezieltes Ausprobieren diesen Werten nähern.

Wir sind mit unserem Forschungsschiff auf einer abgelegenen Südseeinsel gelandet, die von einer eingeführten Kaninchenpopulation beherrscht wird. Wir wollen abschätzen, wie viele der Tiere die Insel bevölkern. Dazu fangen wir 50 Kaninchen, markieren sie und lassen sie wieder laufen, in der Hoffnung, dass diese sich gleichmäßig über der Insel verteilen. Einige Tage später fangen wir erneut 50 Kaninchen und zählen darunter 18 markierte Individuen.
Nun wollen wir mit Hilfe des 95%95 \%-Konfidenzintervalls für die beobachtete relative Häufigkeit der markierten Kaninchen abschätzen, wie groß die Kaninchenpopulation ist.

Lösung:

Als erste Schätzung gehen wir davon aus, dass unsere beobachtete relative Häufigkeit h=1850=0,36=36%h=\frac{18}{50}= 0{,}36 = 36 \% der Wahrscheinlichkeit pp entspricht. Dies würde zu N0=500,36≈139N_0 = \frac{50}{0{,}36}\approx 139 Kaninchen führen.
Die beobachtete relative Häufigkeit ist aber nur ein Punktschätzung für den wahren Anteil pp unter den Kaninchen auf der Insel. Wir suchen ein Untergrenze p1p_1 udn eine Obergrenze p2p_2 zwischen denen die beobachtete relative Häufigkeit hh mit 95%95 \%-iger Wahrscheinlichkeit liegt, also zwei Binomialverteilungen an deren oberer 97,5%97{,}5 \% - Grenze bzw. an deren unterer 2,5%2{,}5 \% - Grenze hh liegt. (2,5%2{,}5 \% bzw. 97,5%97{,}5\% deshalb, weil von den restlichen 5%5\% des 95%95\%-Intervalls die Hälfte ober- und die andere Hälfte unterhalb des Vertrauensbereichs vermutet wird).
Da die Zahlen eher gering sind, nutzen wir nicht die Näherung sondern tasten uns exakt an die Grenzen heran: Für die Untergrenze (für pp) muss gelten, dass 97,5%97{,}5 \% der Ergebnisse unterhalb von 18 Kaninchen liegen, also \[ B_{50,p_1}(X<18) \ge 97{,}5 \% \]
ist. Lässt man sich jetzt für verschiedene Werte von pp kumulierte Binomialverteilungen berechnen erhält man:

$$p_1$$ $$F_{50, p_1}(17)$$
0,229 0,97516
0,230 0,97411

p1≈0,230p_1 \approx 0{,}230 ist also die kleinste Wahrscheinlichkeit, bei der unsere beobachtete Anzahl an markierten Kaninchen noch im 95%95 \% - Vertrauensintervall liegt. Dies ergibt eine Obergrenze für die Anzahl an Individuen von N1=500,230≈217N_1 = \frac{50}{0{,}230} \approx 217.
Analog suchen wir für die Obergrenze der Wahrscheinlichkeit einen Wert für p2p_2 so, dass die beobachtete Anzahl noch gerade im 95%95 \% - Vertrauensintervall liegt, also \[ B_{50,p_2}(X \le 18) \ge 2{,}5 \% \]
Hier erhält man

$$p_2$$ $$F_{50, p_1}(18)$$
0,487 0,02554
0,488 0,02472

0,4870{,}487 bzw. 48,7%48{,}7 \% ist also der größte Wert für die Wahrscheinlichkeit, mit der unsere beobachtete Häufigkeit noch zu 95%95 \% verträglich ist. Dies ergibt eine Untergrenze für die Population von N2=500,487≈103N_2 = \frac{50}{0{,}487} \approx 103.
Wir können also mit einer Wahrscheinlichkeit von 95%95 \% davon ausgehen, dass zwischen 103 und 217 Kaninchen auf der Insel leben. Das Ergebnis scheint sehr ungenau zu sein, lässt aber immerhin eine solide Abgrenzung der Größenordnung (‘wenige Hundert’) zu.
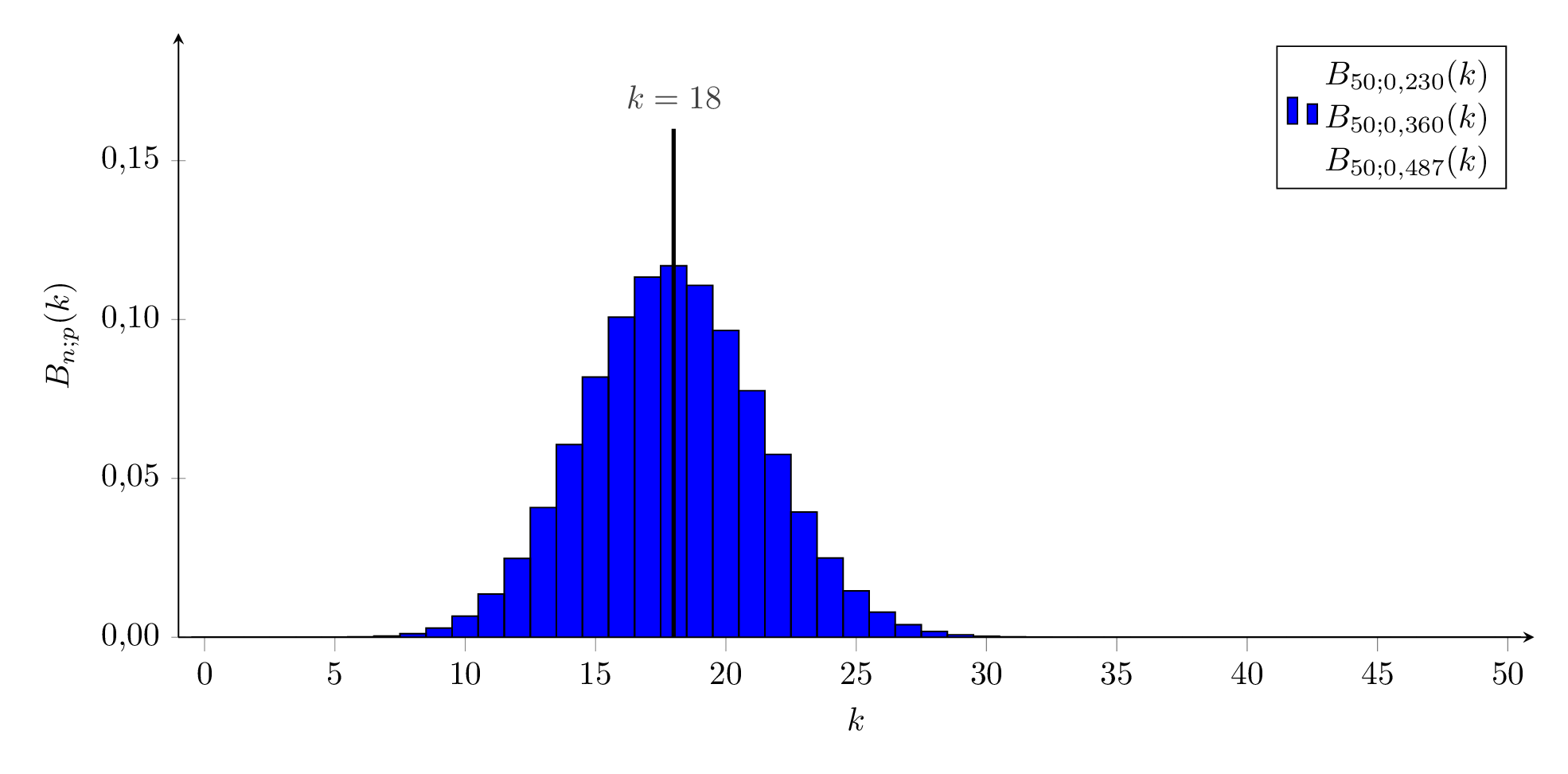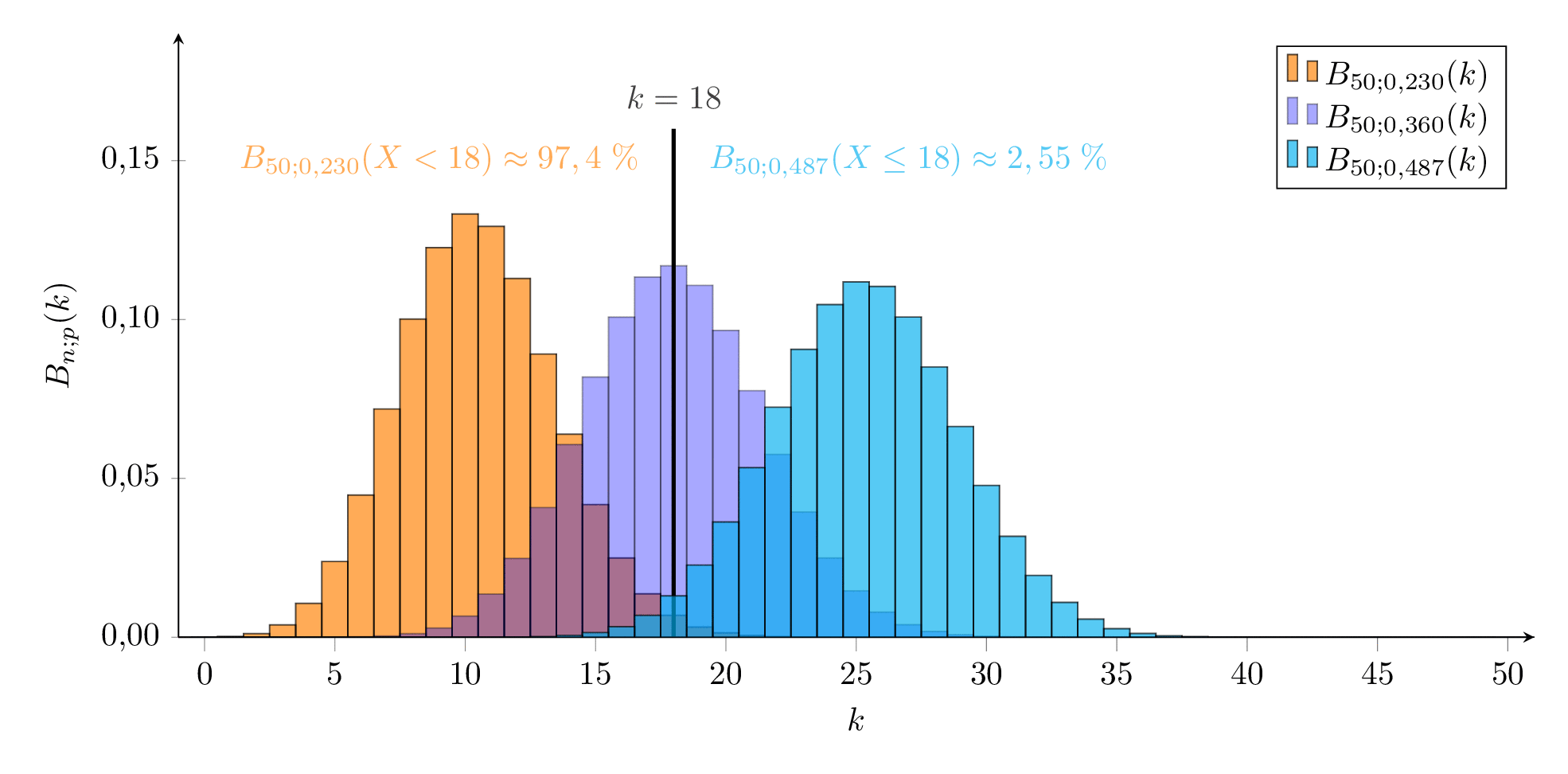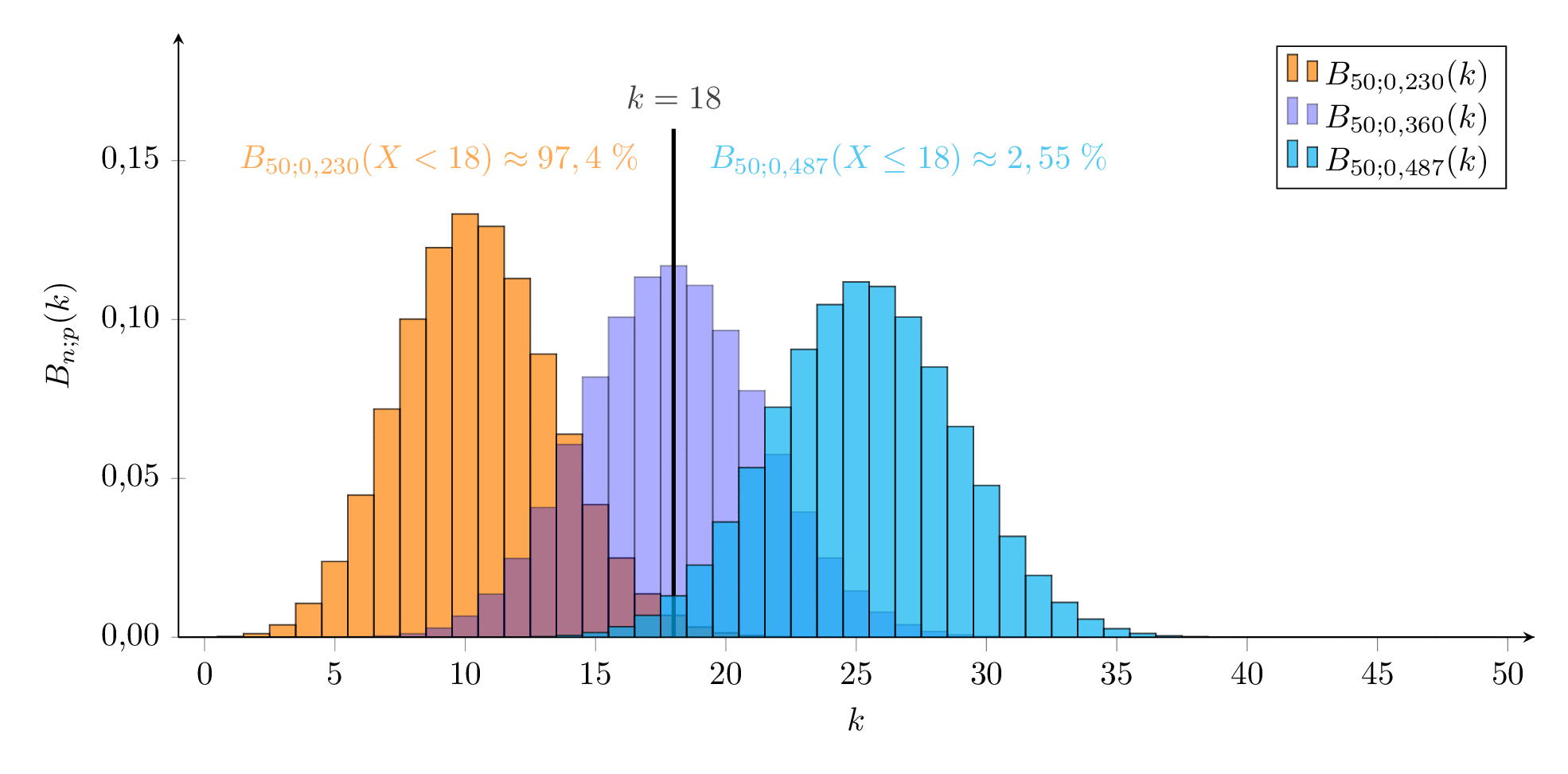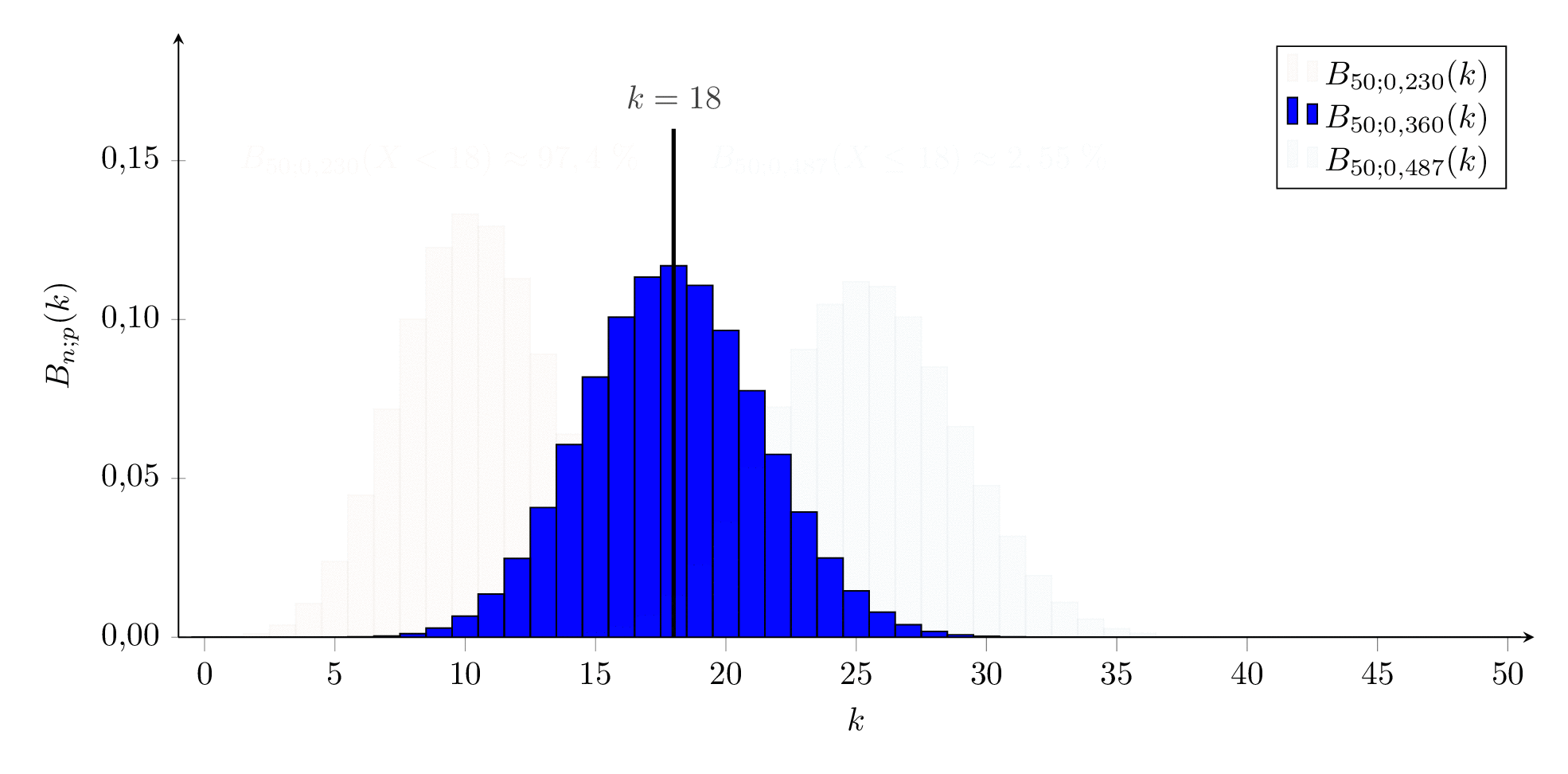
Die beiden ‘Grenzverteilungen’ sind in der folgenden Animation orange bzw. cyan dargestellt, die mit p=h=0,360p=h=0{,}360 in blau. Veranschaulichung des Ergebnisses Mit der Näherungsformel (deren Einsatz hier wegen der kleinen Zahl fragwürdig ist) ergibt sich für die Grenzen der Wahrscheinlichkeit \[ \begin{align*} p_{o/u} &= h \pm c\cdot\sqrt{\frac{h(1-h)}{n}}\\[5pt] p_{o/u} &= 0{,}360 \pm 1{,}96\cdot\sqrt{\frac{0{,}36(1-0{,}36)}{50}}\\[5pt] p_{o/u} &\approx 0{,}360 \pm 0{,}133 \end{align*}\] also pu=0,227p_u = 0{,}227 und po=0,493p_o=0{,}493. In Populationszahlen bedeutet dies:
Als Untergrenze 500,493≈101\frac{50}{0{,}493}\approx 101 und als Obergrenze 500,227≈220\frac{50}{0{,}227}\approx 220.

Wie groß sollte die Stichprobe sein?

Wir wollen auf fünf Prozentpunkte genau ermitteln, mit welchem Ergebnis wir bei der Wahl am kommenden Sonntag (mit einer Wahrscheinlichkeit von 95 %) rechnen können. Dazu wollen wir in der Fußgängerzone eine Umfrage durchführen. Zur Planung wäre es hilfreich zu wissen, wie viele Passanten wir befragen müssen.
Nun, das 95 % -Vertrauensintervall hat eine Breite/Länge von \[ l = 2\cdot c \cdot \sqrt{\frac{h\cdot(1-h)}{n}} \] also den doppelten Abstand vom Mittelwert zur 95 % - Grenze. Wir wollen das Ergebnis auf ±  5  %\pm \;5\;\% genau wissen, das Vertrauensintervall soll also höchstens l=10  %=0,1l=10\;\%=0{,}1 breit sein. Die obige Gleichung können wir nach dem Stichprobenumfang nn auflösen: \[ n = \frac{4\cdot c^2}{l^2}\cdot h\cdot(1-h) \] Dies ist die Mindestanzahl an Personen, die wir fragen müssen um mit 95 %-iger Sicherheit ein Ergebnis mit einer maximalen Ungenauigkeit von ±  5  %\pm \;5\;\% zu erhalten: \[ n \ge \frac{4\cdot c^2}{l^2}\cdot h\cdot(1-h) \quad\quad (\ast) \] Dummerweise haben wir noch keine Idee, wie groß unser Schätzwert (unsere Punktschätzung) hh ist. Gehen wir einfach mal vom ungünstigsten Fall aus. Der Term h⋅(1−h)h\cdot (1-h) hat ein absolutes Maximum von 0,250{,}25 bei h=0,5h=0{,}5 (siehe Abbildung). 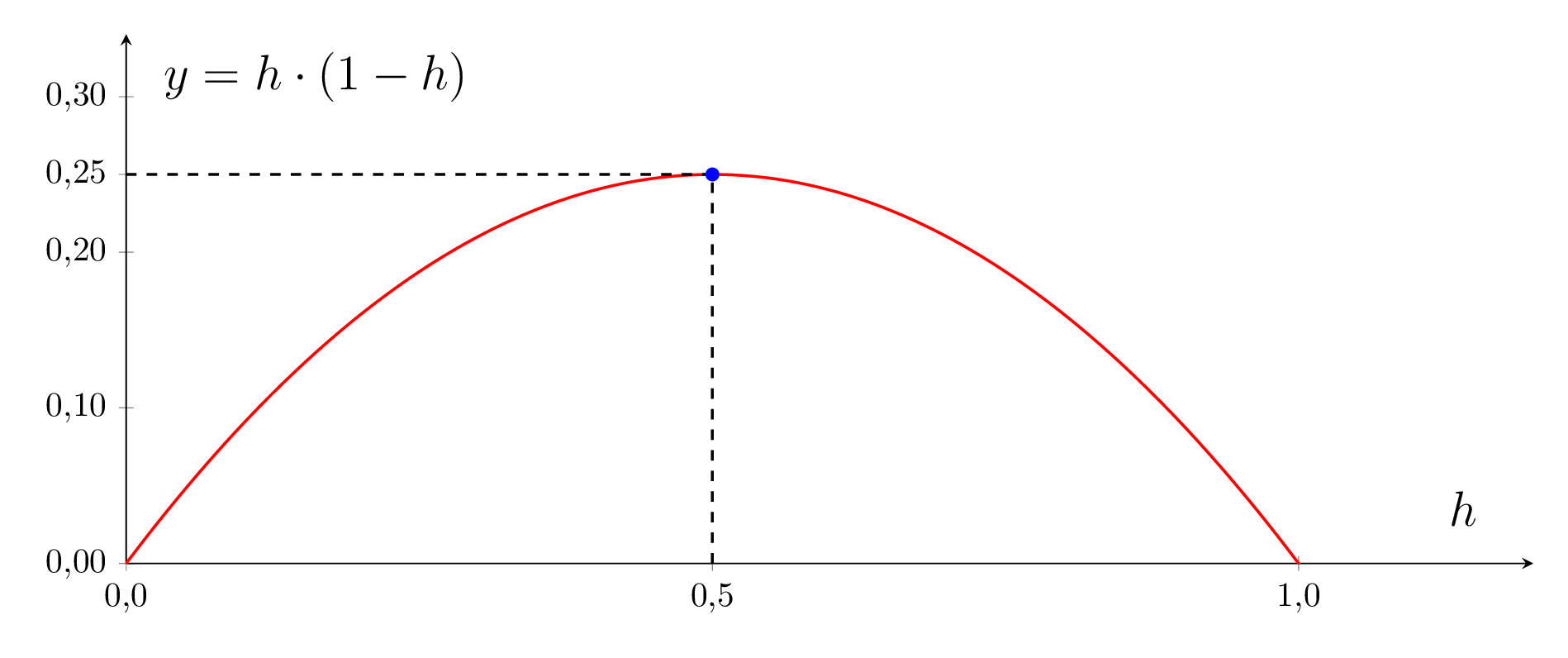Verlauf des Terms $$y=h(1-h)$$ in Abhängigkeit von $$h$$. Im schlimmsten Fall müssen wir also \[ n \ge \frac{4\cdot c^2}{l^2}\cdot 0{,}25=\frac{c^2}{l^2} \] Personen fragen. Da wir eine 95 %-ige Sicherheit haben wollen ist c=1,96c=1,96 und wir wollen es auf 5 % genau haben, also l=0,1l=0{,}1 und somit müssen wir \[ n \ge \frac{1{,}96^2}{0{,}1^2} = 384{,}16 \] also mindestens 385 Passanten befragen um mit mehr als 95 %-iger Wahrscheinlichkeit ein auf ±  5  %\pm\;5\;\% genaues Ergebnis zu erhalten.
Wenn wir davon ausgehen können, dass wir ca. 20 % der Stimmen bekommen, unsere Punktschätzung also 0,2 ist, dann können wir direkt die obige Formel (∗)(\ast) nutzen \[ \begin{align*} n & \ge \frac{4\cdot c^2}{l^2}\cdot h \cdot(1-h) \\[5pt] n & \ge \frac{4\cdot 1{,}96^2}{0{,}1^2}\cdot 0{,}2\cdot(1-0{,}2) \approx 245{,}9 \end{align*} \] und müssen “nur” 246 Passanten befragen, um die gleiche Genauigkeit zu erhalten.

Weitere Beiträge: