Hauptsatz der Differential- und Integralrechnung
24.03.2022Heute wollen wir den Hauptsatz der Differential- und Integralrechnung kennenlernen und beweisen. Im Anschluss wird noch darauf eingagangen, weshalb dieser so nützlich ist und zum Schluss gibt es noch Aufgaben.
Definition Integralfunktion:
Eine Funktion, deren Funktionsvariable (hier: ) eine Grenze des Integrals ist, heißt Integralfunktion.
weist jedem -Wert den (orientierten) Flächeninhalt unter der Kurve zwischen und zu.
Im unteren Beispiel entspricht also der Wert der Integralfunktion an der Stelle dem Flächeninhalt der blauen Fläche.
Als einfaches Beispiel soll die Integralfunktion für die Untergrenze über der Funktion mit betrachtet werden, also \[ I_0(x)=\int_0^x t \; dt\] Beachte, dass die Variable des Integranden umbenannt werden muss (hier in den , da ansonsten nicht eindeutig wäre.
Da es sich bei den Funktionswerten immer nur um Dreiecksflächen handelt sind diese einfach zu berechnen, z.B.
Dies kann auch in einer Wertetabelle zusammengetragen werden:
| $$x$$ | $$0$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ | $$20$$ | $$x_0$$ |
| $$I_0(x)$$ | $$0$$ | $$0,5$$ | $$2$$ | $$4,5$$ | $$8$$ | $$200$$ | $$\frac{1}{2}x_0^2$$ |
Besonders interessant ist die letzte Berechnung. Es scheint, als ergäbe die Ableitung der Integralfunktion gerade den Funktionsterm der Berandungskurve. Wir vermuten also, dass \[ I^{\prime}_a(x)=f(x)\quad \text{mit} \quad I_a(x)=\int_a^x f(t) \; dt \] gilt.
Dies versuchen wir nun zu beweisen:
Die Integralfunktion \[ I_a(x) = \int_a^x f(t) \; dt\] ist ein Maß für die blau eingezeichnete Fläche.
Für die Ableitung nach der h-Methode brauchen wir noch einen Funktionswert an einer Stelle weiter rechts, also für . \[ I_a(x+h) = \int_a^{x+h} f(t) \; dt\] Der Funktionswert der Integralfunktion an der Stelle entspricht dem Inhalt der rot eingezeichneten Fläche:
Zur Bestimmung der Ableitung müssen wir den Differenzenquotienten berechnen: \[ \frac{I_a(x+h)-I_a(x)}{h}\] Die Differenz entspricht geometrisch der Fläche, die durch die Grenzverschiebung von nach hinzukommt (die reinrote Fläche). Diese kann eingegrenzt werden. Sie ist kleiner als das grüne Rechteck aber größer als das gelbe Rechteck :
Die Fläche des Streifens mit der Breite liegt also zwischen den Rechteckflächen: \[ \color{gold}{m\cdot h} \; \le \; \color{#FFB2B2}{I_a(x+h)-I_a(x)} \; \le \; \color{green}{M\cdot h}\] Dividieren durch die Breite des Streifens ergibt den Differenzenquotienten: \[ m \; \le \; \frac{I_a(x+h)-I_a(x)}{h} \; \le \; M\] Wenn nun geht, der Streifen also immer dünner wird, dann rücken die obere Schranke und die untere Schranke immer weiter aufeinander zu. Im Grenzfall sind sie sogar gleich und nehmen den Wert von an der Stelle an, es gilt also \[ m = M = f(x) \]
Für den Differenzenquotienten bedeutet das
\[ \lim_{h \rightarrow 0} \frac{I_a(x+h)-I_a(x)}{h} = I^{\prime}_a(x)\]
also die Definition der Ableitung der Integralfunktion .
Da diese nun sowohl kleiner gleich als auch größer gleich sein muss, kann sie nur gleich sein. Die obige Vermutung ist somit also gezeigt und es gilt:
\[ \color{red}{I^{\prime}_a(x) = f(x)}\]
Anmerkung: Genau betrachtet ist der ‘Beweis’ nicht ganz vollständig, für unsere Ansprüche soll das aber genügen.
Was bringt’s?
“Warum macht ihr Mathelehrer so ein Tamtam darum?” werdet ihr fragen… Nun ja, die Integralfunktion kann durch eine Stammfunktion ausgedrückt werden: \[ I_a(x) = F(x) + c\] Wenn die Ober- und die Untergrenze gleich sind, dann hat die Integralfunktion natürlich den Wert (Die Fläche hat die Dicke 0): \[ I_a(a) = 0\] Wegen ist damit die Integrationskonstante festgelegt durch \[ c = - F(a)\] Damit kann die Integralfunktion durch Stammfunktionen ausgedrückt werden: \[ I_a(x) = F(x) - F(a)\] und insbesondere git für die Obergrenze \[ I_a(b) = F(b) - F(a)\] Dies ist aber gerade der (orientierte) Flächeninhalt unter der Berandungskurve ! Wir können also auch krummlinig begrenzte Flächeninhalte analytisch exakt berechnen!
Hauptsatz der Differential- und Integralrechnung:
ist ist eine beliebige Stammfunktion von . Es gilt: \[ \int_a^b f(x) \; dx = F(b) - F(a)\]
Als Schreibweise hat sich eingebürgert, dass durch eckige Klammern abgekürzt wird und die Ober- bzw. Untergrenze als Indizes an die rechte Klammer geschrieben werden, also so: \[ \int_a^b f(x) \; dx = \Big[ F(x) \Big]_a^b = F(b) - F(a)\] Zum Beispiel können wir damit die von einer Normalparabel eingeschlossene Fläche berechnen: \[ \int_0^2 \underbrace{x^2}_{f(x)} \; dx = \Big[ \underbrace{\frac{1}{3}x^3}_{F(x)} \Big]_0^2 = \underbrace{\frac{1}{3}\cdot2^3 - \frac{1}{3}\cdot 0^2}_{F(b)-F(a)} = \frac{8}{3}\]
Einfluss der Integrationskonstanten
Eine Stammfunktion ist bis auf die Integrationskonstante eindeutig, da beim Ableiten Konstanten verschwinden. Wenn also eine Stammfunktion von ist, dann ist ebenfalls eine Stammfunktion. Beim Berechnen von bestimmten Integralen spielt diese aber keine Rolle, wie das folgende Beispiel zeigt: \[ \begin{align*} \int_a^b f(x) \; dx &= \big[ F(x)+c\big]_a^b \\ &= F(b)+c - \big( F(a)+c\big) \\ &= F(b)\; {\color{red}{ + c }}\; - F(a)\; \color{red}{ - c} \\ &= F(b)-F(a) \end{align*}\]
Ein weiteres Beispiel:
Vorsicht beim Berechnen, das Minuszeichen bei wird häufig vergessen! Im Zweifelsfall eine Klammer mehr setzen!
Aufgaben:
Berechne
\[ \int_1^4 x^3 \; dx = \big[ \frac{1}{4} x^4\big]_1^4 = \frac{4^4}{4} - \frac{1^4}{4} = 63,75\]Berechne
\[ \int_{-1}^2 \mathrm{e}^{2x} \; dx = \Big[ \frac{1}{2} \mathrm{e}^{2x} \Big]_{-1}^2 = \frac{\mathrm{e}^4}{2} - \frac{1}{2\mathrm{e}^2} \approx 27,23\]Berechne
\[ \begin{aligned} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin{(x)} \; dx &= \Big[ -\cos{(x)} \Big]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\ &= -\cos{(\frac{\pi}{2})} - \big(- \cos{(-\frac{\pi}{2})}\big)\\ &= - 0 + 0=0\end{aligned}\]Berechne
\[ \begin{aligned} \int_{0}^{\pi} \sin{(x)} \; dx &= \Big[ -\cos{(x)} \Big]_{0}^{\pi}\\ &= -\cos{(\pi)} + \cos{(0)}\\ &= -(-1) + 1=2\end{aligned}\]Berechne
Zuerst eine Stammfunktion:
Werte an den Integrationsgrenzen:
Integral berechnen:
\
Das kann natürlich auch mit Computerhilfe, z.B. mit WolframAlpha berechnet werden.
Die Eingabe hierfür ist z.B.
integral 4x^3-3x^2+3 from 1 to 3Das war es hierzu. Ich bedanke mich für Eure Aufmerksamkeit und wünsche Euch einen angenehmen Resttag.
Persönliche Bemerkungen zum Hauptsatz:
Der Hauptsatz kann auch anders interpretiert werden, nämlich als
\[ F(b) = F(a) + \int_a^b F^{\prime}(x) \; dx\]
Diese Formulierung liegt ziemlich nahe an einem Grundanliegen der Analysis, nämlich dem Wunsch, Prognosen zu erstellen oder mathematisch ausgedrückt
von vorhandenen Funktionswerten auf neue Funktionswerte zu schließen.
Dazu benötigt man natürlich einen Ausgangspunkt, einen Startwert . Um nun auf den neuen Wert zu schließen braucht man noch die lokale Änderungsrate in der Umgebung, also die Ableitung (engl.: derivative) . Daraus erhält man den neuen Wert . Man leitet also aus vorhandenen Werten mit Hilfe der Ableitung neue Werte ab. Man erhält neue Werte (engl. to derive sth. - etwas bekommen / erhalten).
So gesehen wäre die Umkehrung dieses Prozesses, von den neuen Werten zurück auf die alten zu schließen, sich also alte Werte ableiten.
Daher ist es meines Erachtens unsinnig von ‘aufleiten’ oder gar ‘hochleiten’ (als ginge es hoch und runter) zu sprechen. Genau betrachtet ist dies Formulierung sogar etwas verwirrend.
In der Regel lernt man die Differentialrechnung an ganzrationalen Funktionen kennen und dabei sieht es ja tatsächlich so aus, als würden die Exponenten auf- und absteigen. Spätestens bei der Behandlung von Exponential- oder gar trigonometrischen Funktionen verwirrt dies und vernebelt den Blick auf den wahren Kern der Differential- und Integralrechnung.
 Aus dem Reststück soll nun eine möglichst große, rechteckige Glasplatte zurechtgeschnitten werden.
Aus dem Reststück soll nun eine möglichst große, rechteckige Glasplatte zurechtgeschnitten werden.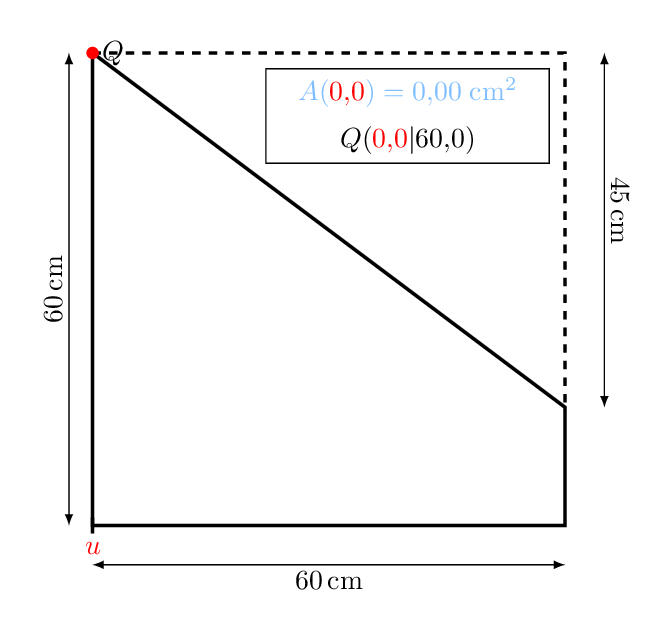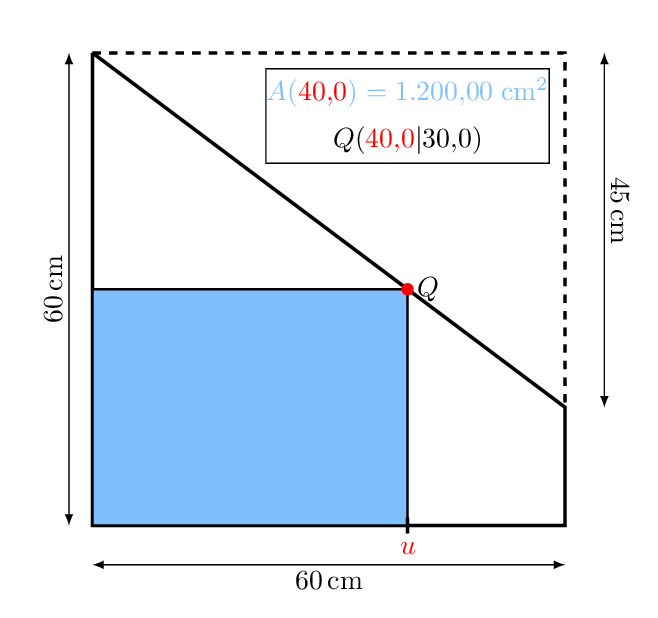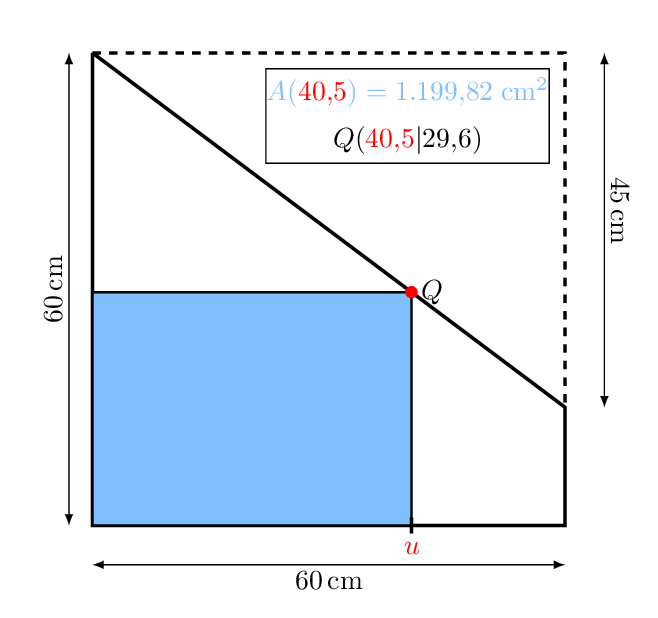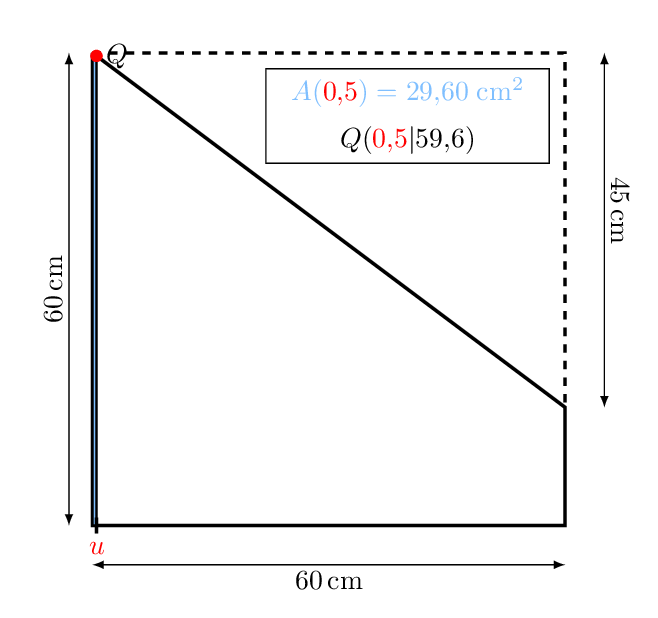
 Mal sehen!
Mal sehen!